During the past two decades, high-order discontinuous Galerkin (DG) methods[1] have been receiving growing interests due to its advantages such as high accuracy, great geometry flexibility, straightforward implementation of h/P adaption and parallel computing.Bassi et al.used a high-order DG method to solve the Euler equations in 1997[2] and then developed BR1 scheme (the first Bassi-Rebay scheme) and BR2 scheme (the second Bassi-Rebay scheme) for solving the Navier-Stokes (N-S) equations[3, 4].Almost at the same time, Oden et al.introduced a high-order DG scheme for the N-S equations without using any auxiliary variables[5].In recent years, the LDG and CDG schemes were also developed for solving the N-S equations in Refs.[6, 7], respectively.Since the DG method is quite similar with the finite volume (FV) method, the numerical fluxes employed in FV method are also widely used in DG method, such as local Lax-Friedrichs (LLF), Roe etc.
As an alternative, the Boltzmann equation-based flux solvers are becoming more and more attractive, such as the kinetic flux vector splitting (KFVS) scheme[8] and the gas-kinetic Bhatnagar-Gross-Krook(BGK) scheme[9, 10].The KFVS scheme usually cannot produce numerical results as accurate as those obtained by Roe[11] or AUSM[12] since the collision process is controlled by numerical time step.The gas-kinetic Bhatnagar-Gross-Krook (BGK) scheme handles the particle collisions using the BGK model and controls the dissipation in the streaming process by the collision time, which gives accurate solutions for both inviscid and viscous flows.However, the use of the Maxwellian function in KFVS and the gas-kinetic Bhatnagar-Gross-Krook (BGK) scheme increases the complexity and reduces the efficiency[8-10].
Recently, some efforts have been made to develop efficient lattice Boltzmann flux solver (LBFS) for compressible flows[13-16], where the inviscid flux at the cell interface is reconstructed using the local solution of one-dimensional compressible lattice Boltzmann model.It is noted that the non-equilibrium part of the distribution function at cell interfaces introduces numerical dissipation, which is helpful for capturing shocks, but not expected in smooth regions, such as boundary layers.
A high-order DG method is employed here to solve both inviscid and viscous flows.Instead of using the conventional numerical inviscid fluxes, a hybrid LBFS is adopted, in which a switch function is introduced to control the numerical dissipation.Numerical results indicate that the hybrid LBFS combining with the high-order DG method can give accurate solutions for both inviscid and viscous flows.
1 DG Discretization of N-S EquationsThe N-S equations in the conservation form can be written as
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot {\mathit{\boldsymbol{F}}_c}\left( \mathit{\boldsymbol{U}} \right) + \nabla \cdot {\mathit{\boldsymbol{F}}_v}\left( {\mathit{\boldsymbol{U}},\nabla \mathit{\boldsymbol{U}}} \right) = \mathit{\boldsymbol{0}} $ | (1) |
where U are the conservation variables and Fc, Fv are the inviscid and viscous flux functions, respectively.
After multiplying a test function V, integrating over the computational domain and performing an integration by parts, the following weak form is obtained
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\int_\mathit{\Omega } {V\mathit{\boldsymbol{U}}{\rm{d}}\mathit{\Omega }} + \int_{\partial \mathit{\Omega }} {V\mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{U}},\nabla \mathit{\boldsymbol{U}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}\delta } - }\\ {\int_\mathit{\Omega } {\nabla V \cdot \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{U}},\nabla \mathit{\boldsymbol{U}}} \right){\rm{d}}\mathit{\Omega }} = 0\;\;\;\;\forall V} \end{array} $ | (2) |
where F(U, ∇U)=Fc(U)+Fv(U, ∇U).By subdividing the computational domain Ω into the non-overlapping elements Ωe, the semi-discrete system is written as
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\int_{{\mathit{\Omega }_e}} {{V_{\rm{h}}}{\mathit{\boldsymbol{U}}_{\rm{h}}}{\rm{d}}{\mathit{\Omega }_e}} + \int_{\partial {\mathit{\Omega }_e}} {{V_{\rm{h}}}\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}\delta } - }\\ {\int_{{\mathit{\Omega }_e}} {\nabla {V_{\rm{h}}} \cdot \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}}} \right){\rm{d}}{\mathit{\Omega }_e}} = 0\;\;\;\;{\rm{for}}\;{V_{\rm{h}}}} \end{array} $ | (3) |
where Uh and Vh are the high-order approximations of U and V
| $ {\mathit{\boldsymbol{U}}_{\rm{h}}}\left( {x,y,t} \right) = \sum\limits_{j = 1}^{N\left( p \right)} {{\mathit{\boldsymbol{u}}_j}\left( t \right){\phi _j}\left( {x,y} \right)} $ | (4) |
| $ {V_{\rm{h}}}\left( {x,y,t} \right) = \sum\limits_{j = 1}^{N\left( p \right)} {{v_j}\left( t \right){\phi _j}\left( {x,y} \right)} $ | (5) |
where φj(x, y) are the basis functions of degree p.Eq.(3) then becomes
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\int_{{\mathit{\Omega }_e}} {{\phi _i}{\mathit{\boldsymbol{U}}_{\rm{h}}}{\rm{d}}{\mathit{\Omega }_e}} + \int_{\partial {\mathit{\Omega }_e}} {{\phi _i}\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}}} \right) \cdot \mathit{\boldsymbol{n}}{\rm{d}}\delta } - }\\ {\int_{{\mathit{\Omega }_e}} {\nabla {\phi _i} \cdot \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}}} \right){\rm{d}}{\mathit{\Omega }_e}} = 0\;\;\;\;\;\;\;\;1 \le i \le N\left( p \right)} \end{array} $ | (6) |
Here, the BR2 scheme[4] is employed, which introduces the following "face" contributions defined as
| $ \int_{{\mathit{\Omega }_e}} {{\phi _i}{\mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}}{\rm{d}}{\mathit{\Omega }_e}} = \int_{\partial {\mathit{\Omega }_e}} {{\phi _i}\left( {{\mathit{\boldsymbol{U}}_{\rm{0}}} - \mathit{\boldsymbol{U}}} \right)\mathit{\boldsymbol{n}}{\rm{d}}\delta } $ | (7) |
where
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\int_{{\mathit{\Omega }_e}} {{\phi _i}{\mathit{\boldsymbol{U}}_{\rm{h}}}{\rm{d}}{\mathit{\Omega }_e}} + }\\ {\int_{\partial {\mathit{\Omega }_e}} {{\phi _i}\mathit{\boldsymbol{H}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}} + {\mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}},\mathit{\boldsymbol{U}}_{\rm{h}}^ + ,\nabla \mathit{\boldsymbol{U}}_{\rm{h}}^ + + \mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}^ + ,\mathit{\boldsymbol{n}}} \right){\rm{d}}\delta } - }\\ {\int_{{\mathit{\Omega }_e}} {\nabla {\phi _i} \cdot \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}} + {\mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}}} \right){\rm{d}}{\mathit{\Omega }_e}} = 0}\\ {1 \le i \le N\left( p \right)} \end{array} $ | (8) |
There are volume and surface integrations in Eq.(8).In order to efficiently solve this equation, Gauss numerical integration method is adopted in this work.The numerical flux H includes the inviscid part Hc(Uh, Uh+, n) and the viscous part Hv(Uh, ∇Uh+r∂Ωe, Uh+, ∇Uh++r+∂Ωe, n).The viscous part can be evaluated by averaging the left and right side of the interface
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_v}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}} + {\mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}},\mathit{\boldsymbol{U}}_{\rm{h}}^ + ,\nabla \mathit{\boldsymbol{U}}_{\rm{h}}^ + + \mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}^ + ,\mathit{\boldsymbol{n}}} \right) = }\\ {\frac{1}{2}\left[ {{\mathit{\boldsymbol{F}}_v}\left( {{\mathit{\boldsymbol{U}}_{\rm{h}}},\nabla {\mathit{\boldsymbol{U}}_{\rm{h}}} + {\mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}}} \right) + {\mathit{\boldsymbol{F}}_v}\left( {\mathit{\boldsymbol{U}}_{\rm{h}}^ + ,\nabla \mathit{\boldsymbol{U}}_{\rm{h}}^ + + \mathit{\boldsymbol{r}}_{\partial {\mathit{\Omega }_e}}^ + } \right)} \right] \cdot \mathit{\boldsymbol{n}}} \end{array} $ | (9) |
As to the inviscid numerical flux, instead of using the widely used LLF flux, Roe flux, AUSM flux, etc., an LBFS is employed in this work.
2 Hybrid Lattice Boltzmann Flux SolverIn the hybrid lattice Boltzmann flux solver, the inviscid flux is evaluated by local reconstruction of solution using one-dimensional lattice Boltzmann model, while the viscous flux is still approximated by conventional smooth function approximation.Thus, in this work, we only consider the evaluation of inviscid flux at the cell interface.For the sake of derivation, the detailed expression of inviscid flux is given first.For two-dimensional case, the inviscid flux in Eq.(7) can be written as
| $ {\mathit{\boldsymbol{H}}_c} = \left[ {\begin{array}{*{20}{c}} {\rho {\mathit{\boldsymbol{U}}_{\rm{h}}}}\\ {\left( {\rho {U_n}{U_n} + p} \right){n_x} - \rho {U_n}{U_\tau }{n_y}}\\ {\left( {\rho {U_n}{U_n} + p} \right){n_y} - \rho {U_n}{U_\tau }{n_x}}\\ {\left( {\rho E + p} \right){U_n}} \end{array}} \right] $ | (10) |
where n=(nx, ny) denotes the unit normal vector on the control surface in the Cartesian coordinate system.ρ, Un, Uτ and p present the density, normal velocity, tangential velocity and the pressure of the mean flow, respectively.E is the total energy defined as
| $ E = e + \frac{1}{2}\left( {U_n^2 + U_\tau ^2} \right) $ | (11) |
where e=p/[(γ-1)ρ] is the potential energy of the mean flow.
In the present work, the inviscid flux Hc is computed by LBFS.It is known that the conservative variables and fluxes at the cell interfaces can be expressed as the summation of lattice velocity, moments and distribution function according to the conservation forms of moments[15].Usually, the distribution function at the cell interface consists of equilibrium part and non-equilibrium part.From the Chapman-Enskog analysis and applying Taylor series expansion in time and physical space, the non-equilibrium part of the distribution function can be approximated by the difference of equilibrium distribution functions at the cell interface and its surrounding point[17, 18].Finally, the inviscid flux at the cell interface can be written as
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_c} = \sum\limits_{i = 1}^4 {{\xi _i}{\mathit{\boldsymbol{\varphi }}_a}{g_i}\left( {0,t} \right)} + }\\ {{\tau _0}\left[ {\sum\limits_{i = 1}^4 {{\xi _i}{\mathit{\boldsymbol{\varphi }}_a}{g_i}\left( { - {\xi _i}\delta t,t - \delta t} \right)} - \sum\limits_{i = 1}^4 {{\xi _i}{\mathit{\boldsymbol{\varphi }}_a}{g_i}\left( {0,t} \right)} } \right] = }\\ {\mathit{\boldsymbol{H}}_c^{\rm{I}} + {\tau _0}\left[ {\mathit{\boldsymbol{H}}_c^{{\rm{II}}} - \mathit{\boldsymbol{H}}_c^{\rm{I}}} \right]} \end{array} $ | (12) |
where τ0 is the dimensionless collision time, δt the streaming time step, ξi the particle velocity in i-direction, and gi(0, t), and gi(-ξiδt, t-δt) are the equilibrium distribution functions at the cell interface and its surrounding points.A non-free parameter D1Q4 model, proposed by Yang et al.[14, 15], is adopted in Eq.(14).φa stands for the moments, which can be written as
| $ {\mathit{\boldsymbol{\varphi }}_a} = {\left( {1,{\xi _i},\frac{1}{2}{\xi ^2} + {e_p}} \right)^{\rm{T}}} $ | (13) |
where
HcⅠ is the flux attributed to the equilibrium distribution function at the cell interface gi(0, t).To obtain gi(0, t), the conservative variables at the cell interface should be computed in advance.According to the compatibility condition and the conservation forms of moments, the density, momentum in the normal direction and energy attributed to normal velocity can be computed by
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_h^ * = {{\left[ {\rho ,\rho {h_0}{U_n},\frac{1}{2}\rho U_n^2 + \rho e} \right]}^{\rm{T}}} = }\\ {\sum\limits_{i = 1}^4 {{\xi _i}{\mathit{\boldsymbol{\varphi }}_a}{g_i}\left( { - {\xi _i}\delta t,t - \delta t} \right)} } \end{array} $ | (14) |
In Eq.(16), the key issue is to evaluate the equilibrium distribution function gi(-ξiδt, t-δt).Like the conventional upwind schemes, it is assumed that a local Riemann problem is formed at the cell interface.Thus, the equilibrium distribution function gi(-ξiδt, t-δt) can be evaluated according to the location of -ξiδt.The non-free D1Q4 model is applied in this paper and gi(-ξiδt, t-δt) can be specified as
| $ {g_i}\left( { - {\xi _i}\delta t,t - \delta t} \right) = \left\{ \begin{array}{l} g_i^{\rm{L}}\;\;\;\;i = 1,3\\ g_i^{\rm{R}}\;\;\;\;i = 2,4 \end{array} \right. $ | (15) |
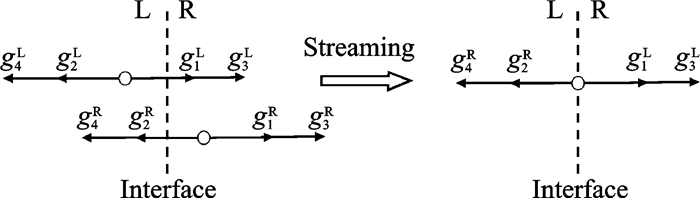
where gLi and giR are the equilibrium distribution functions at the left and right sides of the cell interface, which can be calculated from the corresponding conservative variables Uh and Uh+.The process is illustrated in Fig. 1 and the details can be found in Ref.[15].Substituting Eq.(17) into Eq.(16), we can obtain
| $ \mathit{\boldsymbol{U}}_h^ * = \sum\limits_{i = 1,3} {{\varphi _a}g_i^{\rm{L}}} + \sum\limits_{i = 2,4} {{\varphi _a}g_i^{\rm{R}}} $ | (16) |
|
Fig. 1 Streaming process of non-free parameter D1Q4 model at the cell interface |
In Eq.(18), only the conservative variables, which attributed to the normal velocity, are obtained.To evaluate the tangential velocity at the cell interface, one of the feasible ways can be expressed as
| $ {\left( {\rho {U_\tau }} \right)^ * } = \sum\limits_{i = 1}^4 {{g_i} \cdot \mathit{\boldsymbol{U}}_\tau ^ * } = \sum\limits_{i = 1,3} {g_i^{\rm{L}} \cdot U_\tau ^{\rm{L}}} + \sum\limits_{i = 2,4} {g_i^{\rm{R}} \cdot U_\tau ^{\rm{R}}} $ | (17) |
where Uτ, UτL and UτR are the tangential velocities at the cell interface, the left and right side of cell interface, respectively.With Eqs.(18), (19), the primitive variables ρ*, Un*, Uτ*, p* can be obtained in a straightforward way.By substituting the above primitive variables directly into Eq.(4), the inviscid flux at the cell interface HcⅠ can be expressed as
| $ {\mathit{\boldsymbol{H}}_c} = \left[ {\begin{array}{*{20}{c}} {\rho {\mathit{\boldsymbol{U}}_n}}\\ {\left( {\rho {U_n}{U_n} + p} \right){n_x} - \rho {U_n}{U_\tau }{n_y}}\\ {\left( {\rho {U_n}{U_n} + p} \right){n_y} - \rho {U_n}{U_\tau }{n_x}}\\ {\left( {\rho E + p} \right){U_n}} \end{array}} \right] $ | (18) |
HcⅡ is the flux attributed to the equilibrium distribution function at the surrounding points of the cell interface gi(-ξiδt, t-δt).Since gi(-ξiδt, t-δt) has been determined by Eq.(17), HcⅡ can be computed directly for this case.The mass flux, the momentum flux in the normal direction and the energy flux attributed to the normal velocity across the interface can be written as
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}_c^{{\rm{II}}} = {{\left[ {\rho {U_n},\rho U_n^2 + p\left( {\rho \left( {\frac{1}{2}U_n^2 + e} \right) + p} \right){U_n}} \right]}^{\rm{T}}} = }\\ {\sum\limits_{i = 1,3} {{\xi _i}{\varphi _a}g_i^{\rm{L}}} + \sum\limits_{i = 2,4} {{\xi _i}{\varphi _a}g_i^{\rm{R}}} } \end{array} $ | (19) |
In addition, the contribution of the tangential velocity to the momentum flux in the tangential direction and energy flux can be approximated by
| $ \begin{array}{*{20}{c}} {{{\left( {\rho {U_n}{U_\tau }} \right)}^ * } = \sum\limits_{i = 1}^4 {{\xi _i}{g_i}\left( { - {\xi _i}\delta t,t - \delta t} \right) \cdot \mathit{\boldsymbol{U}}_\tau ^ * } = }\\ {\sum\limits_{i = 1,3} {{\xi _i}g_i^{\rm{L}} \cdot U_\tau ^{\rm{L}}} + \sum\limits_{i = 2,4} {{\xi _i}g_i^{\rm{R}} \cdot U_\tau ^{\rm{R}}} } \end{array} $ | (20) |
| $ \begin{array}{*{20}{c}} {{{\left( {\rho {U_n}U_\tau ^2} \right)}^ * } = \sum\limits_{i = 1}^4 {{\xi _i}{g_i}\left( { - {\xi _i}\delta t,t - \delta t} \right) \cdot {{\left( {U_\tau ^ * } \right)}^2}} = }\\ {\sum\limits_{i = 1,3} {{\xi _i}g_i^{\rm{L}} \cdot {{\left( {U_\tau ^{\rm{L}}} \right)}^2}} + \sum\limits_{i = 2,4} {{\xi _i}g_i^{\rm{R}} \cdot {{\left( {U_\tau ^{\rm{R}}} \right)}^2}} } \end{array} $ | (21) |
By collecting Eqs.(21)-(23), the full expression of HcⅡ can be obtained
| $ \mathit{\boldsymbol{H}}_c^{{\rm{II}}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^4 {{\xi _i}{g_i}} }\\ {\sum\limits_{i = 1}^4 {\xi _i^2{g_i}{n_x}} - \sum\limits_{i = 1}^4 {{\xi _i}{g_i}} \cdot U_\tau ^ * {n_y}}\\ {\sum\limits_{i = 1}^4 {\xi _i^2{g_i}{n_y}} + \sum\limits_{i = 1}^4 {{\xi _i}{g_i}} \cdot U_\tau ^ * {n_x}}\\ {\sum\limits_{i = 1}^4 {{\xi _i}\left( {\frac{1}{2}\xi _i^2 + {e_p}} \right){g_i}} + \frac{1}{2}\sum\limits_{i = 1}^4 {{\xi _i}{g_i}{{\left( {U_\tau ^ * } \right)}^2}} } \end{array}} \right] $ | (22) |
where gi=gi(-ξiδt, t-δt).
2.3 Evaluation of τ0In the hybrid LBFS, τ0 is controlled by an introduced switch function.In the smooth region such as in boundary layer, the switch function takes a value close to zero.However, around the shock wave, it tends to be one.That is, in hybrid LBFS, the numerical dissipation is almost zero in smooth region to simulate accurately the thin boundary layer, and a relatively large numerical dissipation near the strong shock wave is contained to suppress the instability of shock wave.The switch function is defined as
| $ {\tau _0} = \tanh \left( {C\frac{{\left| {{\rho _{\rm{L}}} - {\rho _{\rm{R}}}} \right|}}{{{\rho _{\rm{L}}} + {\rho _{\rm{R}}}}}} \right) $ | (23) |
where tanh(x) is the hyperbolic tangent function, and ρL, ρR the densities at the left and right sides of the cell interface.|ρL-ρR| is the local discontinuity over the cell interface and C is the amplification factor, which is set as C=10 in this work.
3 Numerical ResultsA few benchmark problems are tested with the hybrid LBFS introduced above, including the Sod shock tube, the inviscid flow around a cylinder, the inviscid flow with shocks around the NACA0012 airfoil and the laminar flow around the NACA0012 airfoil.
3.1 Sod shock tube problemThe shock tube problem is a particularly interesting and difficult test case, since it presents an exact solution to the full system of one-dimensional Euler equations containing simultaneously a shock wave, a contact discontinuity and expansion fan.This test case is chosen to demonstrate the flexibility of the LBFS combining with DG method in capturing the shock.The initial value of this problem is set as
| $ \left\{ \begin{array}{l} \left( {{\rho _{\rm{L}}},{u_{\rm{L}}},{p_{\rm{L}}}} \right) = \left( {1,0,1} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 0.5 < x < 0\\ \left( {{\rho _{\rm{R}}},{u_{\rm{R}}},{p_{\rm{R}}}} \right) = \left( {0.125,0,0.1} \right)\;\;\;\;\;\;\;\;0 < x < 0.5 \end{array} \right. $ | (24) |
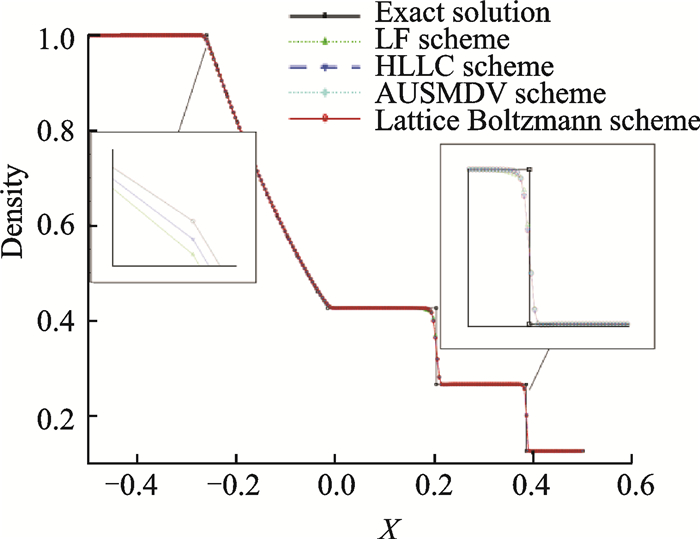
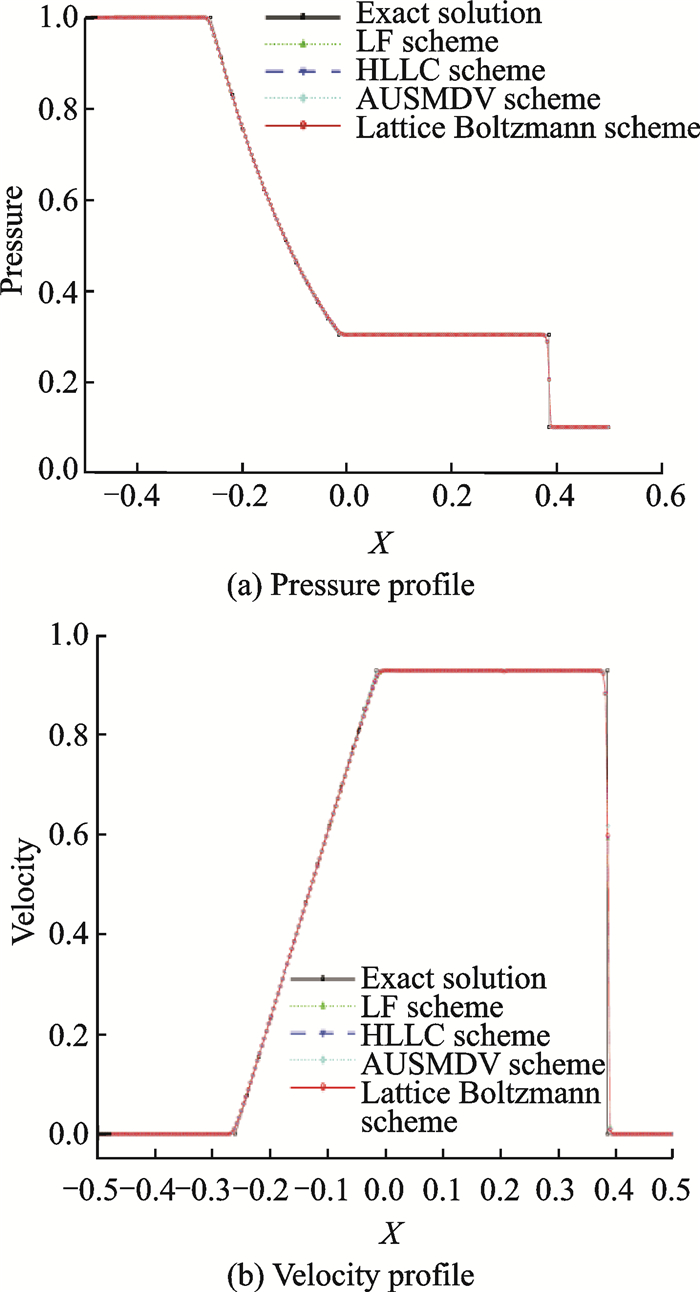
A mesh size of 250 is used for simulation and a third order (p=2) DG method is adopted.Fig. 2 shows the computed density profile obtained by the LBFS scheme (red solid line) at t=0.22.Exact solution (black solid line), the results of Lax-Friedrichs (LF) scheme (green dotted line), HLLC scheme (blue dashed line), AUSMDV scheme (cyan dotted line) are also displayed in Fig. 2.It is observed that the performance of the schemes in capturing the shock is basically the same.However, in the vicinity of the expansion wave, the result of LBFS is the same with that of the AUSMDV scheme, which is steeper than the results of both LF scheme and HLLC scheme, demonstrating a more accurate scheme in dealing with complex flows.Fig. 3 gives the computed profiles of pressure and velocity with different schemes.The results of LBFS match well with those of other schemes and the exact solutions, which demonstrate the capacity of the hybrid lattice Boltzmann flux solver.
|
Fig. 2 Density profile for the 1D Sod shock tube |
|
Fig. 3 Pressure and velocity profiles for 1D Sod shock tube |
3.2 Inviscid flow around a cylinder
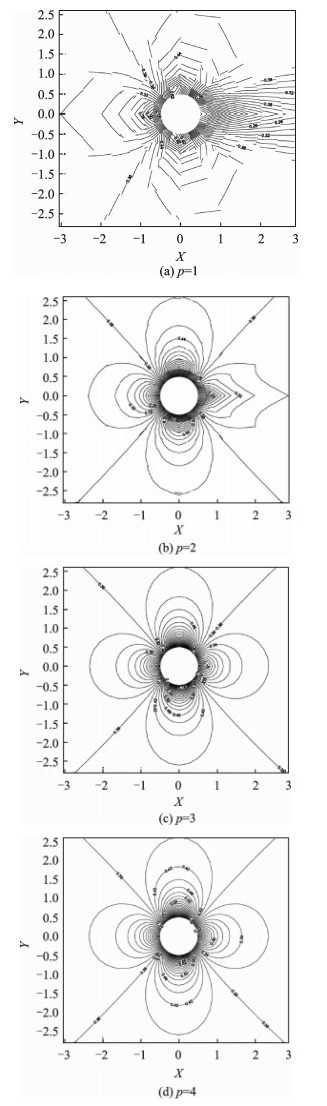
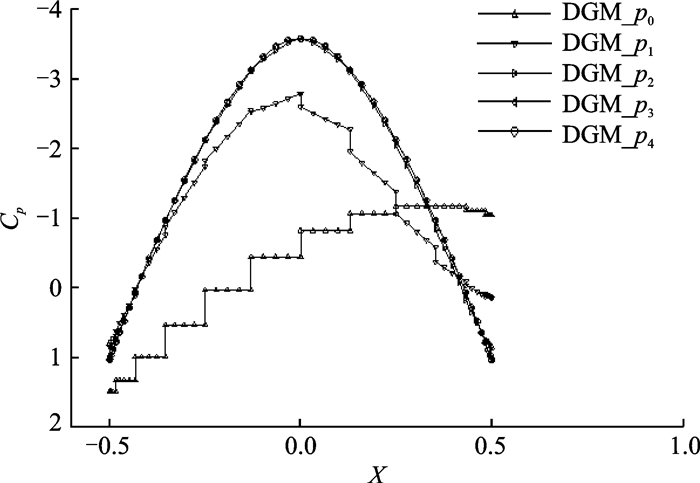
The case of the inviscid flow around a cylinder is used to validate the accuracy of the DG-LBFS scheme.A structured C-grid (16×16) is used in the entire computational domain (Fig. 4), which is very coarse.The obtained Mach number isolines with various orders ranging from 1 to 4 are given in Fig. 5, where the Mach number isolines become smoother with increasing order.The numerical solutions are very close to the analytical solution when p≥3.Fig. 6 displays the distributions of the pressure coefficient Cp.It can be seen that the numerical solution becomes more and more accurate with increasing order and no significant difference can be observed when the order p≥2, which demonstrates the great capacity of the DG-LBFS scheme.
|
Fig. 4 Mesh for inviscid flow around a 2D cylinder |
|
Fig. 5 Mach number contours obtained using different orders |
|
Fig. 6 The distribution of Cp |
3.3 Transonic flow past NACA0012 airfoil
A transonic flow around the NACA0012 airfoil case is used to test the ability of the DG-LBFS method in capturing the shock.The Mach number of the flow condition is 0.85 and the attack angle is 1.25°.
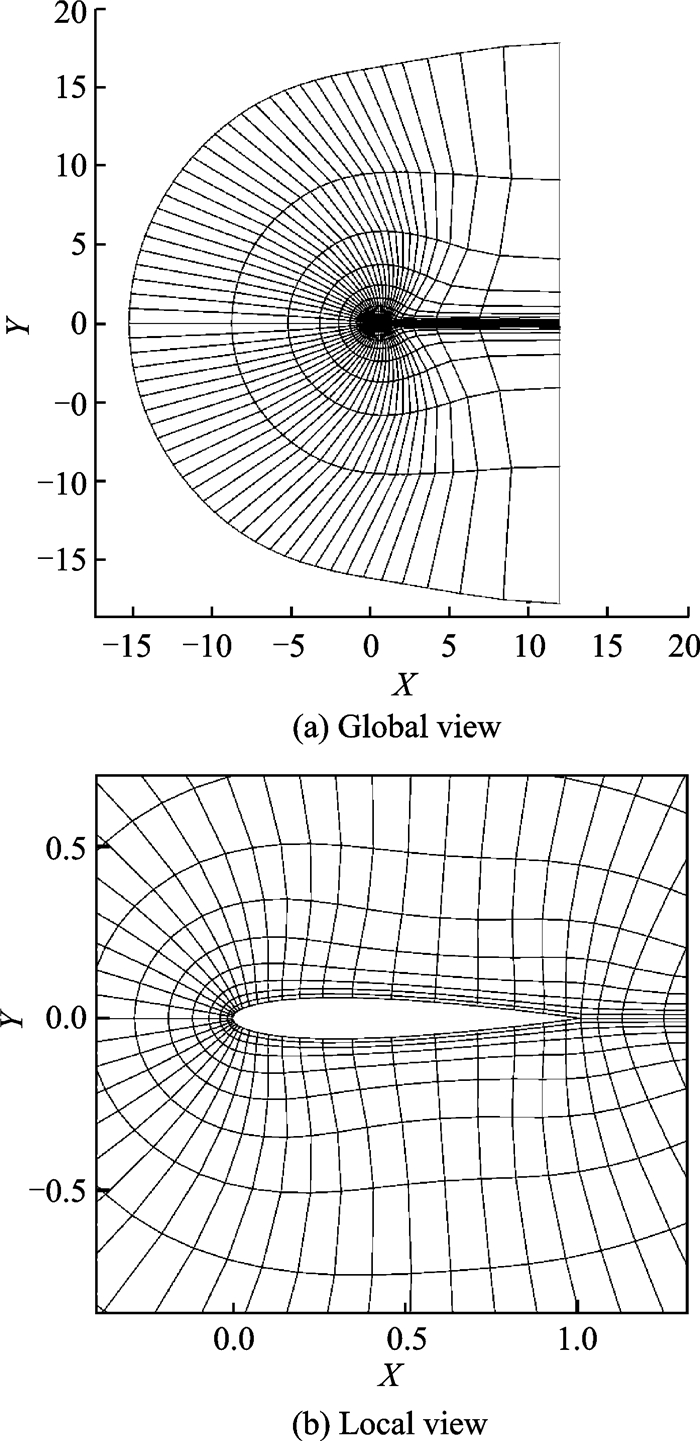
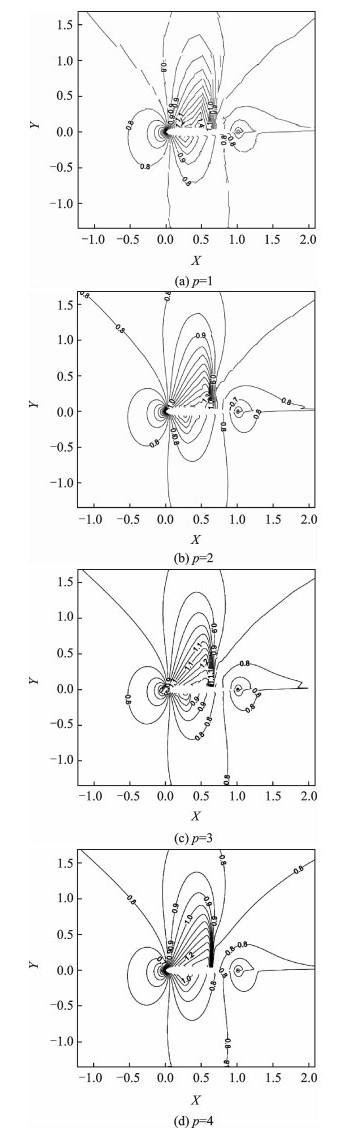
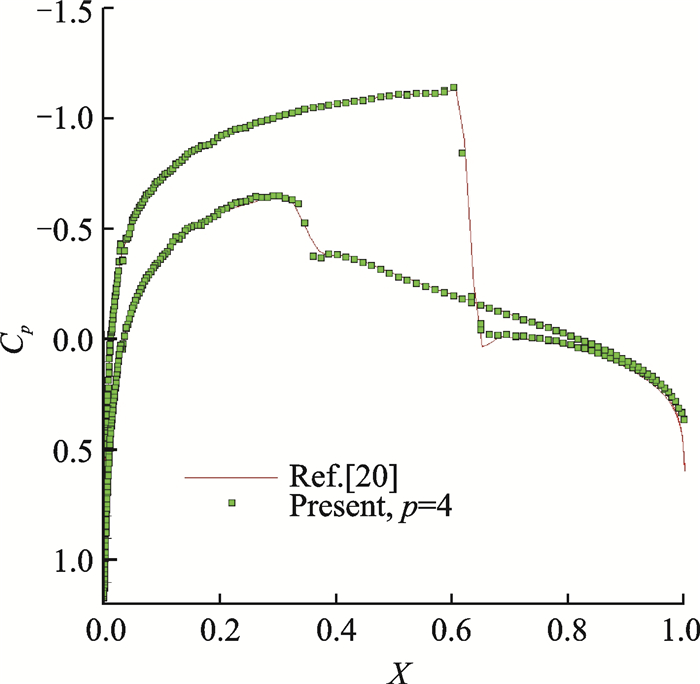
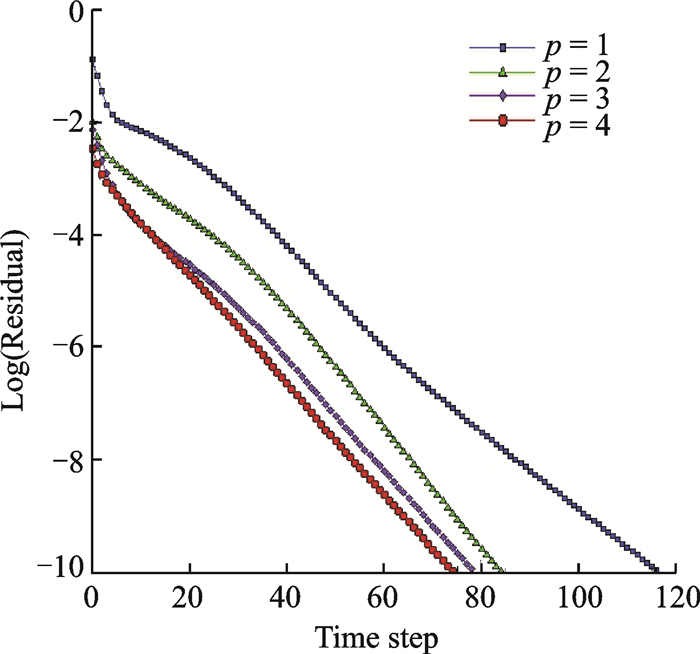
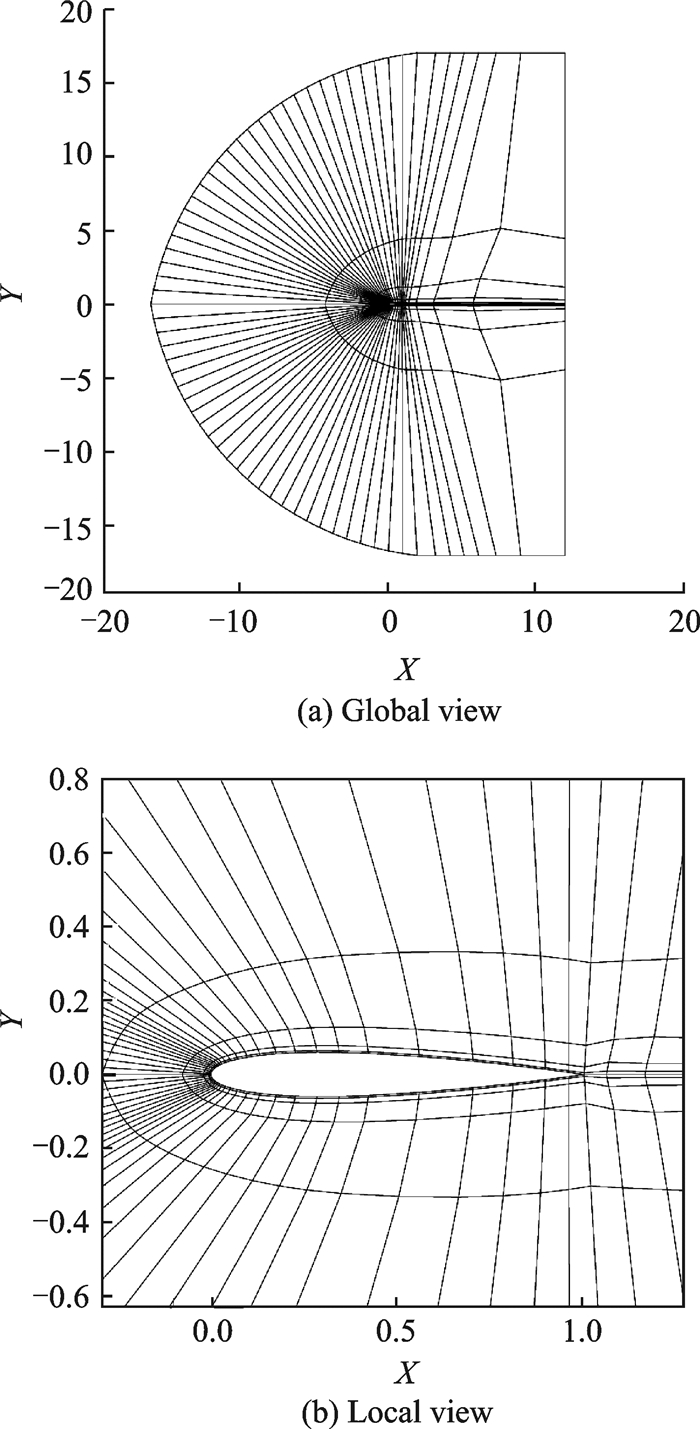
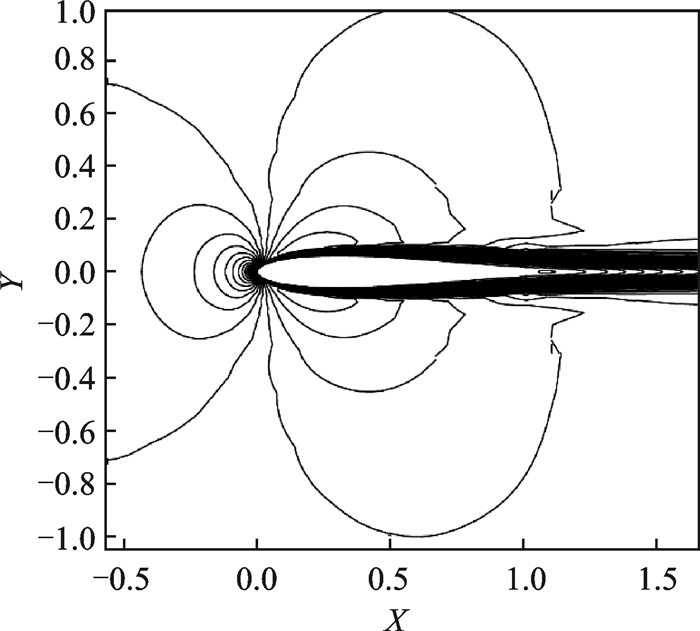
Fig. 7 gives the global view and the local view of the computational mesh, which contains 900 elements in total.Fig. 8 demonstrates the Mach number isolines obtained with different orders.It can be observed that the accuracy becomes higher with increasing orders.The computed pressure coefficient Cp (p=4) is shown in Fig. 9, which depicts a good match compared with the result of Ref.[20].Fig. 10 illustrates the logarithmic density residual versus time step using an implicit method.Converged results can be obtained within several time steps for different orders.Table 1 gives the computed lift coefficient Cl and drag coefficient Cd using DG-LBFS method with different orders.It can be seen that although a coarse grid is used in this case, the results of the DG-LBFS method agree well with that of the finite volume method[20].
|
Fig. 7 Computational mesh for transonic flow past NACA0012 airfoil |
|
Fig. 8 Mach number isolines obtained using different orders |
|
Fig. 9 Cp distribution for transonic flow past NACA012 airfoil (p=4) |
|
Fig. 10 Logarithmic density residual versus time step (p=1-4) for the transonic flow past NACA012 airfoil |
| Table 1 Results of Cl and Cd |
3.4 Laminar flow past NACA0012 airfoil
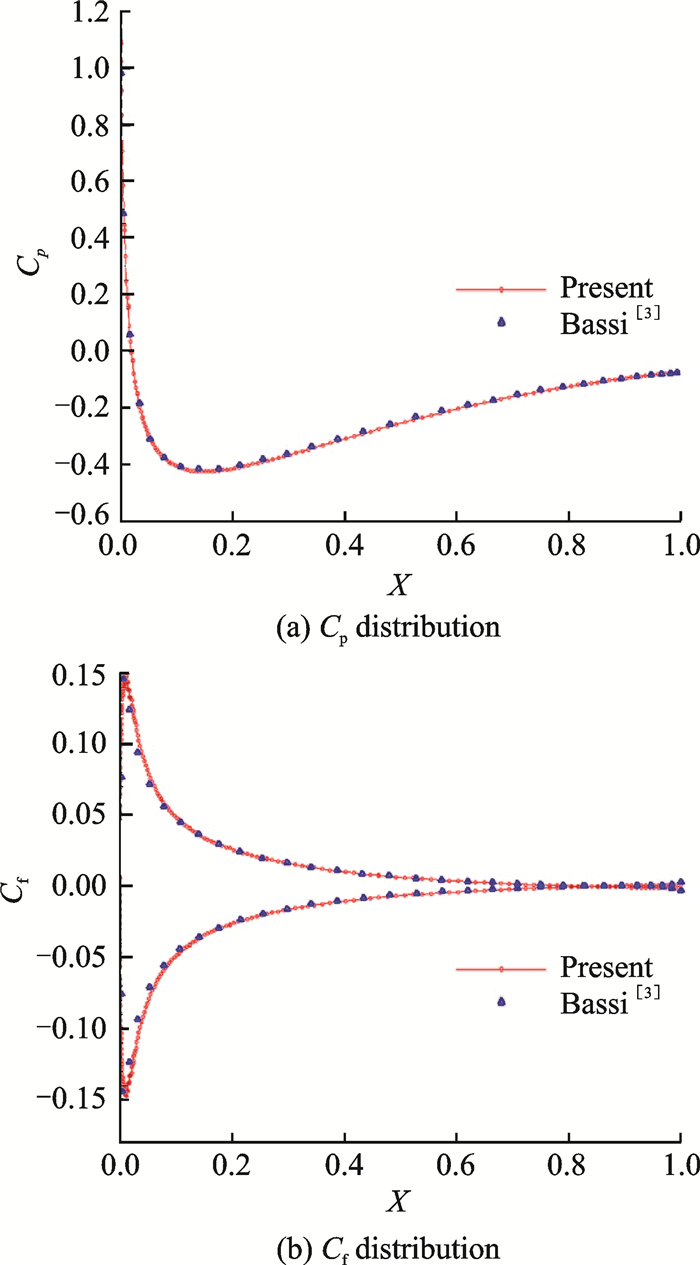
A laminar flow around the NACA0012 airfoil is chosen to test the ability of the DG-LBFS method in capturing the thin boundary layer.The free-stream flow condition is given as Ma∞=0.5 and Re∞=5 000 with an angle of attack α=0°.A coarse mesh with 476 quadrilateral elements is used for this test case as in Fig. 11.The Mach number isolines of order p=4 is displayed in Fig. 12, in which a small recirculation bubble caused by the separation of the flow can be seen in the near-wake region of the airfoil.The results of the pressure coefficient Cp and the friction coefficient Cf are given in Fig. 13, which concur with the results of the Godunov flux function[3].The computed lift coefficient Cl and drag coefficient Cd of different orders using DG-LBFS method are listed in Table 2, which agree well with the results of Refs.[3, 21], showing the capacity of the DG-LBFS method in solving the viscous flow problems.
|
Fig. 11 Computing mesh used for simulation of laminar flow past NACA0012 airfoil |
|
Fig. 12 Computed Mach number isolines of laminar flow past NACA0012 airfoil (p=4) |
|
Fig. 13 Computed Cp and Cf for laminar flow past NACA0012 airfoil |
| Table 2 Comparison of Cl and Cd |
4 Conclusions
The high-order DG method combining with a hybrid lattice Boltzmann flux solver is employed to solve the compressible Euler equations and Navier-Stokes equations.A switch function ranging from 0 to 1 is introduced to control the numerical dissipation when solving the inviscid numerical flux, making the scheme accurate for simulating both smooth flows and the flows with shocks.Numerical results of some benchmark problems indicate that accurate solutions can be obtained even on very coarse grids using the introduced numerical solver.
| [1] |
COCKBURN B, KARNIADAKIS G E, SHU C W. Discontinuous galerkin methods:Theory, computation and applications[M]. Berlin: Springer, 1999.
|
| [2] |
BASSI F, REBAY S. High-order accurate discontinuous finite element solution of the 2D Euler equations[J]. Journal of Computational Physics, 1997, 138: 251-285. DOI:10.1006/jcph.1997.5454 |
| [3] |
BASSI F, REBAY S R. A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations[J]. Journal of Computational Physics, 1997, 131: 267-279. DOI:10.1006/jcph.1996.5572 |
| [4] |
BASSI F, CRIVELLINI A, REBAY S. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω, turbulence model equations[J]. Computers & Fluids, 2005, 34(2): 507-540. |
| [5] |
BAUMANN C E, ODEN J T. A discontinuous hp finite element method for the Euler and Navier-Stokes equations[J]. International Journal for Numerical Methods in Fluids, 1999, 31: 79-95. DOI:10.1002/(ISSN)1097-0363 |
| [6] |
COCKBURN B, SHU C W. The local discontinuous Galerkin method for time-dependent convection-diffusion system[J]. SIAM Journal on Numerical Analysis, 1998, 35(6): 2440-2463. DOI:10.1137/S0036142997316712 |
| [7] |
PERAIRE J, PERSSON P O. The compact discontinuous Galerkin (CDG) method for elliptic problems[J]. SIAM Journal on Scientific Computing, 2008, 30(4): 1806-1824. DOI:10.1137/070685518 |
| [8] |
CHOU S Y, BAGANOFF D. Kinetic flux-vector splitting for the Navier-Stokes equations[J]. Journal of Computational Physics, 1997, 130: 217-230. DOI:10.1006/jcph.1996.5579 |
| [9] |
CHAE D, KIM C, RHO O H. Development of an improved gas-kinetic BGK scheme for inviscid and viscous flows[J]. Journal of Computational Physics, 2000, 158: 1-27. DOI:10.1006/jcph.1999.6400 |
| [10] |
XU K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171: 289-335. DOI:10.1006/jcph.2001.6790 |
| [11] |
ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43: 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [12] |
LIOU M S, STE_EN C J. A new flux splitting scheme[J]. Journal of Computational Physics, 1993, 107: 23-39. DOI:10.1006/jcph.1993.1122 |
| [13] |
JI C Z, SHU C, ZHAO N. A Lattice Boltzmann method-based flux solver and its application to solve shock tube problem[J]. Mod Phys Lett B, 2009, 23: 313-316. DOI:10.1142/S021798490901828X |
| [14] |
YANG L M, SHU C, WU J. Development and comparative studies of three non-free parameter lattice Boltzmann models for simulation of compressible flows[J]. Adv Appl Math Mech, 2012, 4: 454-472. DOI:10.4208/aamm.10-m11146 |
| [15] |
YANG L M, SHU C, WU J. A moment conservation-based non-free parameter compressible lattice Boltzmann model and its application for flux evaluation at cell interface[J]. Computers & Fluids, 2013, 79: 190-199. |
| [16] |
SHU C, YANG Y, YANG L M, et al. Lattice Boltzmann solver:An efficient approach for numerical simulation of fluid flows[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31: 1-15. |
| [17] |
WANG Y, SHU C, TEO C J. Thermal lattice Boltzmann flux solver and its application for simulation of incompressible thermal flows[J]. Computers & Fluids, 2014, 94: 98-111. |
| [18] |
WANG L M, SHU C, WU J. A simple distribution function-based gas-kinetic scheme for simulation of viscous incompressible and compressible flows[J]. Journal of Computational Physics, 2014, 274: 611-632. DOI:10.1016/j.jcp.2014.06.033 |
| [19] |
GUO Z L, SHU C. Lattice Boltzmann method and its applictions in engineering[M]. World Scientific Publishing, 2013.
|
| [20] |
ECONOMON T D, PALACIOS F, COPELAND S R, et al. SU2:An open-source suite for multiphysics simulation and design[J]. AIAA Journal, 2016, 54(3): 828-846. DOI:10.2514/1.J053813 |
| [21] |
JAWAHAR P, KAMATH H. A high-resolution procedure for Euler and Navier-Stokes computations on unstructured grids[J]. Journal of Computational Physics, 2000, 164: 165-203. DOI:10.1006/jcph.2000.6596 |
 2018, Vol. 35
2018, Vol. 35


