Flight dynamics model(FDM) is commonly controlled by the flight control system (FCS). The degree of approximation to real aircraft with its operation environment has a critical influence on FCS design. Besides, a proper FDM is also an important foundation for investigations conducted on atmospheric disturbance, aircraft's control surface jam, abnormal configuration and other safety problems in special flights.
Atmospheric disturbance has strong influence on flight quality and flight safety. To cope with the flight dynamic problems considering turbulent wind, the small-disturbance model was firstly adopted for performance analysis[1]. However, A number of studies conducted at NASA indicate that flight states under turbulent wind seriously deviate from trim points, and the small-disturbance model cannot describe the special flight states accurately[2]. To remedy the model's shortcoming, a varied control gain is calculated by gain scheduling among several linear models in commercial aircraft [3].
Frost et al. first proposed the dynamics equation with wind effects, and in his study, the turbulent wind effects on airspeed and flight path equation were derived in body coordinate system[4]. In real-time flight simulations, the model can be integrated numerically to address wind effects. However, for the sake of its complexity, some advanced control algorithms, such as feedback linearization and nonlinear dynamic inversion cannot be adopted.
Visser studied an FDM with wind effects in the flight path coordinates, and proposed an optimal control strategy to address the recovery from wind shear[5]. However, the model is based on constant wind hypothesis and mass-point assumption. Consequently, flight path angle can be described by FDM directly, but the angle of attack is acquired by geometry relation. This FDM does not accord with the principle that the turbulent wind should firstly have effects on aerodynamic angle.
In recent years, aiming at modern gain scheduling and feedback linearization, LPV model has been put forward. LPV model has the similar characteristics to those of the linear model, but the coefficient matrix is a set of functions of scheduling variables. Defined by system states, the scheduling variables can be updated by scheduling algorithm. The LPV FDM, built by the rational order reduction and specific scheduling variable selection, is capable of capturing the transient response in special flights, and can be operated under varying flight conditions within a large range.
The LPV method has been applied to the dynamics modeling of large-scale civil aircraft[6], UAV[7, 8], battle aircraft[9, 10] and near space hypersonic vehicle[11]. There are three methods for LPV modeling, which are Jacobian linearization[6, 7], state transformation[6, 9] and function substitution[6, 10]. Jacobian linearization is actually one-order approximation at FDM's trim point. In state transformation method, non-scheduling variables and control inputs are expressed in the form of continuous differentiable functions, and can be calculated by its partial derivatives. These two methods need to build up a trim map with system states interpolated. Research results indicate that model precision is dependent on the selected trim points. In respect to the above two methods, the precision is satisfactory only within a small range around trim points, and the extrapolation ability is conservative[6, 9]. In function substitution, the nonlinear characteristics of the system are described by decomposing function, and the function can be solved by optimization procedure. Based on function substitution, LPV model provides the preferable extrapolation ability and approximates the nonlinear system dynamics more accurately than the former two methods[6, 10].
This paper studies one particular kind of LPV FDM, in which the wind effects are taken into account. Firstly, the dynamic equations which address the influence of wind disturbance are derived in the wind frame. Next, the LPV model is formulated using function substitution, and furthermore, genetic algorithm(GA) is utilized to solve the nonlinear multi-dimensional optimal problem for the proposed substitute function. Numerical results of dynamic response and simulations of aircraft flying through turbulent wind are presented to validate the proposed LPV model in the presence of wind effects.
1 Flight Dynamics Modeling with Wind Effects 1.1 Nonlinear flight dynamics modeling with wind effects in wind frameAircraft's aerodynamic forces are calculated under wind coordinate frame. Turbulent wind firstly has effects on airspeed V, angle of attack α and angle of sideslip β, and then changes aerodynamic forces. As a result, dynamic equations under wind coordinate can illustrate wind effects directly. In wind-free situation, force equations under wind coordinate are[3]
| $ \left\{ \begin{array}{l} m\dot V = {F_{\rm{T}}}\cos \left( {\alpha + {\alpha _{\rm{T}}}} \right)\cos \beta - D + m{g_1}\\ m\dot \beta V = - {F_{\rm{T}}}\cos \left( {\alpha + {\alpha _{\rm{T}}}} \right)\sin \beta - C + m{g_2} - mV{r_{\rm{w}}}\\ m\dot \alpha V\cos \beta = - {F_{\rm{T}}}\sin \left( {\alpha + {\alpha _{\rm{T}}}} \right) - L + m{g_3} + mV{q_{\rm{w}}} \end{array} \right. $ | (1) |
where FT is the engine thrust; αT the engines' installation angle; L, D, C are the lift, the drag and the side force, respectively. The transition matrix Ceb is used to describe the states transition from ground coordinate system to body frame, while Cbw is used to transit state from body frame to wind frame. These transition matrices are given as
| $ \mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{b}} = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{\cos \theta \sin \psi }&{ - \sin \theta }\\ {\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi }&{\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }&{\sin \varphi \cos \theta }\\ {\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi }&{\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi }&{\cos \varphi \cos \theta } \end{array}} \right] $ | (2) |
| $ \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{w}} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\sin \beta }&{\sin \alpha \cos \beta }\\ { - \cos \alpha \sin \beta }&{\cos \beta }&{ - \sin \alpha \sin \beta }\\ { - \sin \alpha }&0&{\cos \alpha } \end{array}} \right] $ | (3) |
The relationship between body frame and wind frame for airspeed vector is
| $ \left[ {\begin{array}{*{20}{c}} {{V_x}}\\ {{V_y}}\\ {{V_z}} \end{array}} \right] = {\left( {\mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{w}}} \right)^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} V\\ 0\\ 0 \end{array}} \right] $ | (4) |
In addition, angular velocities under body frame [p, q, r]T can be transformed to wind frame [pw, qw, rw]T, which is
| $ \left[ {\begin{array}{*{20}{c}} {{p_{\rm{w}}}}\\ {{q_{\rm{w}}}}\\ {{r_{\rm{w}}}} \end{array}} \right] = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{w}}\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] $ | (5) |
It can be found that there is a triangular relationship among ground speed VE, airspeed VW and wind speed WE
| $ {\mathit{\boldsymbol{V}}_{\rm{E}}} = {\mathit{\boldsymbol{V}}_{\rm{W}}} + {\mathit{\boldsymbol{W}}_{\rm{E}}} $ | (6) |
In wind-free situation, VE= VW. Wind speed vector WE=[WxE, WyE, WzE]T is given in ground coordinate and it is abbreviated as [Wx, Wy, Wz]T. In order to add the turbulent wind into wind coordinate system, the following transformation is deduced
| $ \left[ {\begin{array}{*{20}{c}} {{W_{x{\rm{w}}}}}\\ {{W_{y{\rm{w}}}}}\\ {{W_{z{\rm{w}}}}} \end{array}} \right] = \mathit{\boldsymbol{C}}_{\rm{b}}^{\rm{w}}\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{b}}\left[ {\begin{array}{*{20}{c}} {{W_x}}\\ {{W_y}}\\ {{W_z}} \end{array}} \right] $ | (7) |
By inserting Eqs.(5), (7) into Eq.(1), the force equation with wind effects can be obtained
| $ \left\{ \begin{array}{l} \dot V = \frac{{{F_{\rm{T}}}}}{m}\cos \left( {\alpha + {\alpha _{\rm{T}}}} \right)\cos \beta - \frac{D}{m} - {\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)_{11}}{{\dot W}_x} - \\ \;\;\;\;\;\;{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)_{12}}{{\dot W}_y} - {\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)_{13}}\left( {{{\dot W}_z} - g} \right)\\ \dot \beta = - \frac{{{F_{\rm{T}}}}}{{mV}}\cos \left( {\alpha + {\alpha _{\rm{T}}}} \right)\sin \beta - \frac{\mathit{\boldsymbol{C}}}{{mV}} + m{g_2} + \\ \;\;\;\;\;\;\;p\sin \alpha - r\cos \alpha - \frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{21}}}}{V}{{\dot W}_x} - \\ \;\;\;\;\;\;\;\frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{22}}}}{V}{{\dot W}_y} - \frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{23}}}}{V}\left( {{{\dot W}_z} - g} \right)\\ \dot \alpha = - \frac{L}{{mV\cos \beta }} + q - \left( {p\cos \alpha + r\sin \alpha } \right)\tan \beta - \\ \;\;\;\;\;\;\frac{{{F_{\rm{T}}}}}{{mV\cos \beta }}\sin \left( {\alpha + {\alpha _{\rm{T}}}} \right) - \frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{31}}}}{{V\cos \beta }}{{\dot W}_x} - \\ \;\;\;\;\;\;\frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{32}}}}{{V\cos \beta }}{{\dot W}_y} - \frac{{{{\left( {\mathit{\boldsymbol{C}}_{\rm{e}}^{\rm{w}}} \right)}_{33}}}}{{V\cos \beta }}\left( {{{\dot W}_z} - g} \right) \end{array} \right. $ | (8) |
Compared with the force equations described in body frame[12], Eq.(8) shows the direct influence of turbulent wind on [V, α, β]T. Besides, wind effects can be directly inserted into navigation equations
| $ \left\{ \begin{array}{l} {{\dot x}_{\rm{E}}} = {V_x}\cos \theta \cos \psi + {V_y}\left( { - \cos \tilde \omega \sin \psi + } \right.\\ \;\;\;\;\;\;\left. {\sin \tilde \omega \sin \theta \cos \psi } \right) + {V_z}\left( {\sin \tilde \omega \sin \psi + } \right.\\ \;\;\;\;\;\;\left. {\cos \tilde \omega \sin \theta \cos \psi } \right) + {W_x}\\ {{\dot y}_{\rm{E}}} = {V_x}\cos \theta \sin \psi + {V_y}\left( {\cos \tilde \omega \cos \psi + } \right.\\ \;\;\;\;\;\;\left. {\sin \tilde \omega \sin \theta \sin \psi } \right) + {V_z}\left( { - \sin \tilde \omega \cos \psi + } \right.\\ \;\;\;\;\;\;\left. {\cos \tilde \omega \sin \theta \sin \psi } \right) + {W_y}\\ {{\dot h}_{\rm{E}}} = - {V_x}\sin \theta + {V_y}\sin \tilde \omega \cos \theta + \\ \;\;\;\;\;\;{V_z}\cos \tilde \omega \cos \theta - {W_z} \end{array} \right. $ | (9) |
The B747-100 aircraft with open source aerodynamic data is selected as the research objective in this paper. Taking the lift coefficient as an example, there are 14 aerodynamic derivatives[13, 14], and the complete expression can be used for hi-fidelity flight simulation. For dynamic analysis and control law design, it is common to simplify the aerodynamic model by selecting the dominant aerodynamic derivatives. The dominant lift aerodynamic derivatives of B747-100 applied in this article are
| $ \begin{array}{*{20}{c}} {{C_L} = {C_{{L_{{\rm{Basic}}}}}} + \frac{{{\rm{d}}{C_L}}}{{{\rm{d}}\tilde {\dot \alpha }}}\left( {\frac{{\dot \alpha \bar c}}{{2V}}} \right) + \frac{{{\rm{d}}{C_L}}}{{{\rm{d}}\hat q}}\left( {\frac{{q\bar c}}{{2V}}} \right) + }\\ {{K_\alpha }\frac{{{\rm{d}}{C_L}}}{{{\rm{d}}{\delta _{{{\rm{e}}_i}}}}}{\delta _{{{\rm{e}}_i}}} + {K_\alpha }\frac{{{\rm{d}}{C_L}}}{{{\rm{d}}{\delta _{{{\rm{e}}_{\rm{o}}}}}}}{\delta _{{{\rm{e}}_{\rm{o}}}}}} \end{array} $ | (10) |
Normally, these aerodynamic derivatives have a direct relation with V, α, β, hE, and they are obtained via interpolation based on the aerodynamic data. Different types of wind disturbance are represented by various wind speed vectors, which could change corresponding to the space and time distinctively. They can be described as atmospheric turbulence model, microburst wind shear model, etc[12]. Taking microburst windshear as example, there are harmonic Soesman model[5], vortex ring model[12] and some other engineering models. In this paper, the vortex ring model is adopted, and furthermore, similar to aerodynamic derivatives query, real-time turbulent wind vector can be obtained according to the flight path parameters.
2 GA-LPV Modeling 2.1 LPV modeling by function substitutionIn order to adopt the function substitution method, the nonlinear system is described as
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot z}}}\\ {\mathit{\boldsymbol{\dot w}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( \mathit{\boldsymbol{z}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( \mathit{\boldsymbol{z}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{z}}\\ \mathit{\boldsymbol{w}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]\mathit{\boldsymbol{u}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_1}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{k}}_2}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]} \end{array} $ | (11) |
where z(t)∈ Rnz is the scheduling state; w(t)∈ Rnw the non-scheduling state; and u(t)∈ Rnu the control input. Using trim value and deviator, Eq.(11) is further written as
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \eta }}}_z}}\\ {{{\mathit{\boldsymbol{\dot \eta }}}_w}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_z}}\\ {{\mathit{\boldsymbol{\eta }}_w}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}} + {\mathit{\boldsymbol{\eta }}_z}} \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_u} + \mathit{\boldsymbol{F}}} \end{array} $ | (12) |
where F is the decomposing function for (ηz, ztrim, wtrim, utrim), and the complete form is
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{z}}_{{\rm{trim}}}}}\\ {{\mathit{\boldsymbol{w}}_{{\rm{trim}}}}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]{\mathit{\boldsymbol{u}}_{{\rm{trim}}}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{k}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{k}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right] \buildrel \Delta \over = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_1}\left( \mathit{\boldsymbol{z}} \right)}\\ {{\mathit{\boldsymbol{f}}_2}\left( \mathit{\boldsymbol{z}} \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_z}} \end{array} $ | (13) |
The key point of function substitution LPV modeling is to rebuild Eq.(13) as a function of scheduling variables. Substituting Eq.(13) into Eq.(12) yields
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \eta }}}_z}}\\ {{{\mathit{\boldsymbol{\dot \eta }}}_w}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{11}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right) + {\mathit{\boldsymbol{f}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{12}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{21}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right) + {\mathit{\boldsymbol{f}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}&{{\mathit{\boldsymbol{A}}_{22}}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\eta }}_z}}\\ {{\mathit{\boldsymbol{\eta }}_w}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)}\\ {{\mathit{\boldsymbol{B}}_2}\left( {{\mathit{\boldsymbol{\eta }}_z} + {\mathit{\boldsymbol{z}}_{{\rm{trim}}}}} \right)} \end{array}} \right]{\mathit{\boldsymbol{\eta }}_u}} \end{array} $ | (14) |
Taking the longitudinal LPV modeling for example, [V, α, hE]T are selected as scheduling variables which mainly have effects on the aerodynamic derivatives. Some non-scheduling variables, such as pitch angle θ, are expressed using first-order approximation. As a result, the longitudinal state space model is described by an affine parameter dependent form with a residual element
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\dot \alpha }\\ {\dot V}\\ {{{\dot h}_{\rm{E}}}}\\ {\dot q}\\ {\Delta \dot \theta }\\ {\dot x} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&0&{{A_{14}}}&{{A_{15}}}&0\\ 0&0&0&{{A_{24}}}&{{A_{25}}}&0\\ 0&{{A_{32}}}&0&0&{{A_{35}}}&0\\ 0&0&0&{{A_{44}}}&0&0\\ 0&0&0&1&0&0\\ 0&{{A_{62}}}&0&0&{{A_{65}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \alpha \\ V\\ {{h_{\rm{E}}}}\\ q\\ {\Delta \theta }\\ x \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{B_{11}}}&0&{{B_{13}}}\\ 0&0&{{B_{23}}}\\ 0&0&0\\ {{B_{41}}}&{{B_{42}}}&{{B_{43}}}\\ 0&0&0\\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _{\rm{e}}}}\\ \sigma \\ T \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{C_{11}}}\\ {{C_{12}}}\\ 0\\ 0\\ 0\\ 0 \end{array}} \right]\left[ g \right] + \left[ {\begin{array}{*{20}{c}} {{D_{11}}}\\ {{D_{12}}}\\ 0\\ {{D_{14}}}\\ 0\\ 0 \end{array}} \right]} \end{array} $ | (15) |
In this article, the entries of the matrix in Eq.(15) can be built up according to the B747-100 aerodynamic data[13, 14]. Restricted by space, only the matrix element related to turbulent wind is shown as follows
| $ \begin{array}{*{20}{c}} {{A_{14}} = 1 - \frac{{\bar qS\bar c}}{{2m{{\left( {V + f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right.} \right)}^2}}}}\\ {\left( {1.45 - 1.8{x_{cg}}} \right) \cdot \frac{{{\rm{d}}{C_L}}}{{{\rm{d}}q}}} \end{array} $ |
| $ {A_{24}} = - \frac{{\bar qS}}{m}\frac{{\partial {C_{{D_{{\rm{Mac}}}}}}}}{{\partial q}}\left| {_{{\rm{trim}}}} \right. - f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_z}}} \right. $ |
| $ {B_{11}} = - \frac{{{K_\alpha }\bar qS}}{{m\left( {V + f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right.} \right)}}\left( {\frac{{{\rm{d}}{C_L}}}{{{\rm{d}}{\delta _{{{\rm{e}}_i}}}}} + \frac{{{\rm{d}}{C_L}}}{{{\rm{d}}{\delta _{{{\rm{e}}_{\rm{o}}}}}}}} \right) $ |
| $ {B_{13}} = - \frac{1}{{m\left( {V + f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right.} \right)}} \cdot \left( {\sin \alpha + 0.0436 \cdot \cos \alpha } \right) $ |
| $ \begin{array}{*{20}{c}} {{C_{11}} = \frac{1}{{\left( {V + f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right.} \right)}}\left( {\sin \alpha \sin {\theta _{{\rm{trim}}}} + } \right.}\\ {\left. {\cos \alpha \cos {\theta _{{\rm{trim}}}}} \right)} \end{array} $ |
| $ {D_{11}} = - \frac{{\bar qS{C_{{L_{{\rm{basic}}}}}}\left( {\alpha ,M} \right) + mf'\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_z}}} \right.}}{{m\left( {V + f\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right.} \right)}} $ |
| $ {D_{12}} = - \frac{{\bar qS}}{m}{C_{{D_{{\rm{Mac}}}}}}\left( {\alpha ,{q_{{\rm{trim}}}},M,{h_{\rm{E}}}} \right) - f'\left( {x,{h_{\rm{E}}}} \right)\left| {_{{W_x}}} \right. $ |
where f(x, h) is the wind field. Wind field is related to flight path and altitude, which can be calculated by a turbulent wind model.
According to function substitution method, the residual element in Eq.(15) should be described by scheduling variables. Furthermore, an optimization objective function should be found to minimize the error between LPV system and nonlinear systems. Rewrite C and D matrixes defined in Eq.(15) into the function substitution format, the complete form is shown as follows
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{F_1}}\\ {{F_2}}\\ {{F_3}}\\ {{F_4}}\\ {{F_5}}\\ {{F_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&{{A_{32}}}&0\\ 0&0&0\\ 0&0&0\\ 0&{{A_{62}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _{{\rm{trim}}}}}\\ {{V_{{\rm{trim}}}}}\\ {{h_{{\rm{trim}}}}} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {{B_{11}}}&0&{{B_{13}}}\\ 0&0&{{B_{23}}}\\ 0&0&0\\ {{B_{41}}}&{{B_{42}}}&{{B_{43}}}\\ 0&0&0\\ 0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\delta _{{{\rm{e}}_{{\rm{trim}}}}}}}\\ {{\sigma _{{\rm{trim}}}}}\\ {{T_{{\rm{trim}}}}} \end{array}} \right] + \left[ \begin{array}{l} {C_{11}}\\ {C_{12}}\\ 0\\ 0\\ 0\\ 0 \end{array} \right]\left[ g \right] + \left[ \begin{array}{l} {D_{11}}\\ {D_{12}}\\ 0\\ {D_{14}}\\ 0\\ 0 \end{array} \right] \buildrel \Delta \over = }\\ {\left[ {\begin{array}{*{20}{c}} {{F_{1\alpha }}}&{{F_{1V}}}&{{F_{1h}}}\\ {{F_{2\alpha }}}&{{F_{2V}}}&{{F_{2h}}}\\ {{F_{3\alpha }}}&{{F_{3V}}}&{{F_{3h}}}\\ {{F_{4\alpha }}}&{{F_{4V}}}&{{F_{4h}}}\\ {{F_{5\alpha }}}&{{F_{5V}}}&{{F_{5h}}}\\ {{F_{6\alpha }}}&{{F_{6V}}}&{{F_{6h}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \alpha }\\ {\Delta V}\\ {\Delta {h_{\rm{E}}}} \end{array}} \right]} \end{array} $ | (16) |
The main objective of function substitution is to approximate Eq.(16) by reconstructing a new equation which is shown at the end of Eq.(16).
2.3 Heuristic optimization by genetic algorithmThere are various realizations of the coefficient matrix in Eq.(16). It is necessary to select a group of optimal coefficients to push the LPV model approaching the nonlinear system as much as possible. Taking the solution of F1 in Eq.(16) as an example, scheduling states [V, α, hE]T can be divided by a grid as i×j×k. According to Refs. [6, 15], it is feasible to solve F1α, F1V, F1h by linear programming with absolute value constraints. However, with the increasement of scheduling variables and grids refinement, particularly when the system shows strong nonlinearity, it is difficult to obtain the optimal solution only by linear programming. In this paper, genetic algorithm (GA) is adopted to solve the optimization problem, and it follows that
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\min \ \ \ \varepsilon \\ {\rm{s}}.\;{\rm{t}}.\\ \begin{array}{*{20}{c}} {{F_1}\left( {{\alpha _i},{V_j},{h_k}} \right) = \left( {{\alpha _i} - {\alpha _{{\rm{trim}}}}} \right){F_{1{\alpha _{ijk}}}} + }\\ {\left( {{V_j} - {V_{{\rm{trim}}}}} \right){F_{1{V_{ijk}}}} + \left( {{h_k} - {h_{{\rm{trim}}}}} \right){F_{1{h_{ijk}}}} \cdot }\\ {\sum\limits_{i,j,k} {\left| {{F_1}\left( {{\alpha _i},{V_j},{h_k}} \right) - \left( {{\alpha _i} - {\alpha _{{\rm{trim}}}}} \right){F_{1\alpha }} - } \right.} }\\ {\left. {\left( {{V_j} - {V_{{\rm{trim}}}}} \right){F_{1V}} - \left( {{h_k} - {h_{{\rm{trim}}}}} \right) \cdot {F_{1h}}} \right| \le \varepsilon } \end{array} \end{array} $ | (17) |
In the process of applying the GA optimization, it is essential to determine the number of initial population, which is the matrix coefficient in Eq.(17). Encoding and random initialization will be done to the population. Next, the fitness function is treated as the optimization objective of Eq. (17) and furthermore, fitness calculation is imposed on the initial population. During the iterating process, the optimal solution can be obtained if the value of fitness function is lower than the initial threshold value.
The nonlinear FDM selected in the paper is complicated, and the computation and time cost of GA will increase as the grid points increases. However, Eq.(17) can be solved off-line. Once the LPV model was built up, the optimization process is no longer needed.
3 GA-LPV FDM Performance AnalysisThe direct method to estimate the performance of LPV FDM is to compare the dynamic response of LPV FDM with that of the nonlinear FDM. In this section, the dynamic response will be firstly tested. Then, the response of flying through microburst wind field will be compared between LPV FDM and nonlinear FDM.
Based on the B747-100 nonlinear FDM, the aircraft can be trimmed into a stable flight condition as shown in Table 1.
| Table 1 Trim state of B747-100 in level flight |
The grid is primarily partitioned based on α∈[0, 5, 10], V∈[160, 200, 240], hE∈[6 500, 7 000, 7 500], and the LPV FDM can be obtained according to Section 2.
3.1 Response comparison between GA-LPV FDM and nonlinear FDMThe elevator is deflected according to Fig. 1. The dynamic response of GA-LPV FDM and nonlinear FDM is shown as follows.
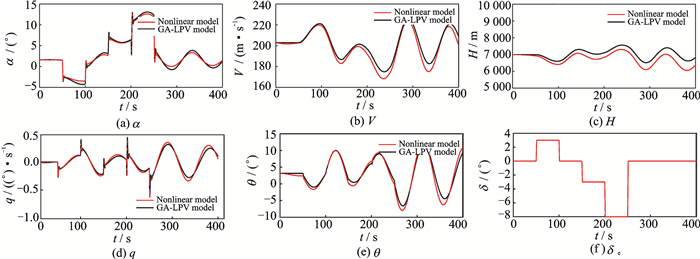
|
Fig. 1 Control response comparison between GA-LPV FDM and nonlinear FDM |
The simulation results show that GA-LPV FDM can approach the instantaneous dynamics of nonlinear FDM. When the angle of attack is high as shown in Fig. 1(a), the GA-LPV FDM can approach the dynamic response of nonlinear FDM accurately only by extrapolation, although it is on the boundary of aerodynamic envelope. Therefore, it shows that the GA-LPV FDM has a good adaptation in a large range. Therefore, it shows good adaptation in a wide range. Furthermore, two sets of varying eigenvalues of GA-LPV FDM system matrices are plotted in Fig. 2.

|
Fig. 2 Eigenvalues variation of GA-LPV FDM |
The varying eigenvalues of the GA-LPV FDM show that the short-period and phugoid characteristics vary accordingly with the changes of scheduled variables. This advantage provides the GA-LPV FDM with better performance than small-disturbance model.
Apart from the above simulation, this paper also presents other multiple sets of tests to analyze the dynamic response. In order to further quantify the discrepancies between GA-LPV FDM and the nonlinear model, the following performance index is given
| $ J = \sum\limits_{i = 1}^{{n_x}} {\frac{1}{{{t_f}}}\sum\limits_{t = 0}^{{t_f}} {\frac{{{{\left[ {{x_{nl\left( i \right)}}\left( t \right) - {x_{{\rm{LPV}}\left( i \right)}}\left( t \right)} \right]}^2}}}{{{S_i}}}} } $ | (18) |
where xnl(i) and xLPV(i) are system states with respect to each model, and Si the normalization coefficient. Comparison results based on the test excitations of elevator deflection δe, horizontal stabilizer deflection σ and thrust change T are given in Table 2.
| Table 2 Response comparison for GA-LPV FDM and nonlinear FDM |
Comparison analysis by several test data shows that GA-LPV FDM can approach the nonlinear system perfectly.
3.2 Response comparison for flying through turbulent windThis section will test the dynamic response of GA-LPV FDM and nonlinear FDM for approaching and landing in the wind field. A microburst wind field is generated by ring vortex and Rankine vortex principle according to Ref.[12]. A real-time wind vector is obtained by searching space positions. The nonlinear system was trimmed at gliding constantly from the height value 1 000 m. Simulation results are shown in Fig. 3.

|
Fig. 3 Wind response comparison between GA-LPV FDM and nonlinear FDM |
The nonlinear dynamic system is based on the dynamic equations derived in Section 2, in which the dynamic response of an aircraft operating in wind disturbance is precisely captured. Fig. 3 illustrates the GA-LPV FDM has the similar response to those of nonlinear FDM generally, but it cannot "follow" the instantaneous state change at local state. Further, the altitude response is inconsistent. Within the range of the nonlinear dynamic response, the grid is reselected as α∈[0, 5, 10], V∈[200, 240, 280], hE∈[0, 500, 1 000], and the updated simulation results are shown in Fig. 4.
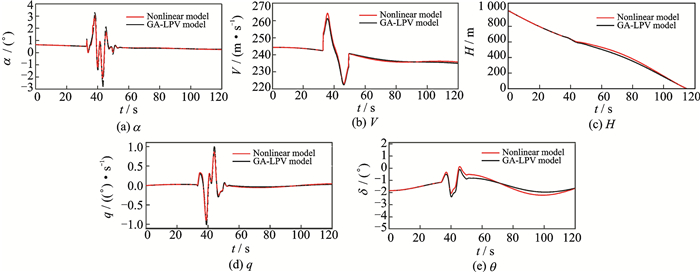
|
Fig. 4 Wind response comparison by grid optimization |
Applying the performance index in Eq.(18), the discrepancy of the dynamic response of the two models reduces from 0.068 621 to 0.012 139. The results indicate that the GA-LPV FDM system performance would further approximate the nonlinear dynamic response based on a proper grid partition of scheduling variables.
4 ConclusionsThis paper derives an FDM which addresses the influence of wind disturbance in wind coordinate system. Based on the proposed FDM, a function substitution LPV FDM is realized, in which the decomposing function is solved by GA. The dynamic response analysis shows that the GA-LPV model approach the nonlinear FDM well because it can reflect the instantaneous dynamics and flight states change in a wide range. According to the simulations of flying through wind field, GA-LPV FDM with wind effects also shows similar performance to nonlinear FDM.
Based on this research, future works would include the following aspects:
(1) The current achievements will be applied to analyze the safety problems in special flight. Based on aerodynamic data, the scheduled variables can be specifically selected to design the LPV FDM for special flight, and then, the analysis and simulations can be conducted. To deal with the strong nonlinearities in the local dynamic system, a local LPV FDM can be obtained by refining local grid partition.
(2) For robust gain scheduling control design, the LPV FDM plays an important role to extend other studies on control algorithms. Besides, the affine parameter dependent LPV FDM will also reduce the algorithm complexity in designing gain scheduled controllers.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No.U1533120), the Aeronautical Science Foundation of China (No. 20158052057), and the Fundamental Research Funds for the Central Universities(No.NS2015066).
| [1] |
XIAO Yelun, JIN Changjiang. Flight principle in atmosphereic disturbance[M]. Beijing: National Defense Industry Press, 1993. (in Chinese)
|
| [2] |
JORDAN T, LANGFORD W, BELCASTRO C, et al. Development of a dynamically scaled generic transport model testbed for flight research experiments: NASA 23-728-30-33[R]. USA: NASA, 2003.
|
| [3] |
BRIAN L S. Aircraft control and simulation[M]. New York: John Wiley and Sons, 2003.
|
| [4] |
FROST W, BOWLES R L. Wind shear terms in the equations of aircraft motion[J]. Journal of Aircraft, 1984, 21(11): 866-872. DOI:10.2514/3.45056 |
| [5] |
VISSER H G. Optimal lateral-escape maneuvers for microburst encounters during final approach[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1234-1240. DOI:10.2514/3.21338 |
| [6] |
MARCOS A, BALAS G J. Development of linear parameter varying models for aircraft[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(2): 218-228. DOI:10.2514/1.9165 |
| [7] |
ZONG Qun, JI Yuehui, DOU Liqian, et al. LPV model reduction of UAV lateral system[J]. Control and Decision, 2010, 25(6): 948-952. (in Chinese) |
| [8] |
VANEK B, PENI T, SZABO Z. Fault tolerant LPV control of the GTM UAV with dynamic control allocation[C]//AIAA Guidance, Navigation, and Control Conference. [S.l.]: AIAA, 2014: 341-346.
|
| [9] |
PAPAGEORGIOU G, GLOVER K. Design, analysis and flight testing of a robust gain scheduling controller for the vaac harrier: TR-368[R]. UK: University of Cambridge, 2000.
|
| [10] |
BHATTACHARYA R, BALAS G J, KAYA M A, et al. Nonlinear receding horizon control of an F-16 aircraft[J]. Journal of Guidance, Control, and Dynamics, 2002, 25(5): 924-931. DOI:10.2514/2.4965 |
| [11] |
HUANG Y, SUN C, QIAN C, et al. ILinear parameter varying switching attitude control for a near space hypersonic vehicle with parametric uncertainties[J]. nternational Journal of Systems Science, 2014, 46(16): 1-13. |
| [12] |
GAO Zhenxing, GU Hongbin, LIU Hui. Real-time simulation of large aircraft flying through microburst wind field[J]. Chinese Journal of Aeronautics, 2009, 22(5): 459-466. DOI:10.1016/S1000-9361(08)60126-0 |
| [13] |
HANKE C R. The simulation of a large jet transport aircraft volume Ⅰ: Mathematical model: NASA CR-1756[R]. USA: NASA, 1971.
|
| [14] |
HANKE C R, NORDWALL R D. The simulation of a jumbo jet transport aircraft volume Ⅱ: Modeling data: NASA CR-114494[R]. USA: NASA, 1970.
|
| [15] |
YU Jianqiao, HU Guohuai, BIE Yanhua. Development of missle quasi-linear model using funtion substitution method[J]. Transaction of Beijing Institute of Technology, 2009, 29(5): 390-393. (in Chinese) |
 2018, Vol. 35
2018, Vol. 35


