0 Introduction
During the past decades, many researchers have focused on various kinds of control methods, especially the ones rely on specific mathematical models, to improve the control of quad-rotors.For example, reduced model based PID and linear quadratic (LQ) methods[1-3], accurate model based nonlinear feedback linearization method[4-7], and nonlinear dynamic inversion[8] were developed. Some other methods were proposed for allowing partial model information to vary within certain range[9-10]. Though there are some methods relying on no detailed model[11-12], they are quit tedious in design process.
Only a few works have discussed the flight of ordinary-sized and micro-sized quad-rotors under external uncertainties using the above mentioned methods[12-17].In addition, their mechanisms on disturbances rejection mainly focus on enhancing the robustness of the control system and resisting instantaneous uncertainties, but they take no consideration on persistent ones, which may be a usual case in reality.
Therefore, according to the above discussion, in the design of control system of nano quad-rotors (NQRs), two problems need to be addressed under persistent uncertainties. Firstly, controllers should have good robustness. Secondly, controllers should not rely on accurate model.To solve those problems, in this paper, a robust INDI method based on the TNDI method and the linear extended state observer (LESO) is developed to design the altitude and attitude control law for NQRs. As known to all, NDI-based controller has some advantages[18], for instance, its structure is very simple, only a few parameters need to be tuned and their determination is very simple according to the bandwidth of state variables. Generally, the control effect in the TNDI method completely depends on the accuracy of the model. As discussed above, the internal and external uncertainties cannot be modeled precisely or some even cannot be modeled. To overcome this drawback of TNDI, the LESO is introduced into NDI to estimate the uncertainties using only input and output data of the control system. Hence, the uncertain dynamics in the controllers can be predicted and then counteracted. To show the superiority of the INDI-based method, a numerical comparison with TNDI was carried out.
1 Structure of Altitude and AttitudeControl Systems for NQRsBefore modeling NQRs, two coordinates (inertial and body), some forces, moments and geometrical parameters are introduced first, as shown in Fig. 1.

|
Fig. 1 Coordinates description of NQRs |
In Fig. 1, OEExEyEz represents the inertial coordinate, in which Ex and Ey are on the horizontal plane and Ex is perpendicular to Ey, Ez is perpendicular to the horizontal determined by the right-hand rule. OBBxByBz represents the body coordinate centered at the center of gravity of the NQRs. Bx is the normal flight orientation, By is positive to starboard in the horizontal plane and Bz is orthogonal to the plane BxOBBy.
The nonlinear movement equations of NQRswithout uncertainties are expressed as
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot P}} = \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{\dot v}} = g \cdot {\mathit{\boldsymbol{e}}_z} - \frac{1}{m}\mathit{\boldsymbol{R}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) \cdot {T_r} \cdot {\mathit{\boldsymbol{e}}_z}\\ \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }} = \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) \cdot \mathit{\boldsymbol{\omega }}\\ \mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{I}}^{ - 1}}\left( { - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{I\omega }} + \tau } \right) \end{array} \right. $ | (1) |
where P, v ∈R3 represent position and velocity of NQRs in inertial frame, respectively, m and g represent mass of NQRs and gravitational constant, respectively, ω=[p, q, r]T∈ R3 is angular velocity in body coordinate, Θ =[φ, θ, ψ]T∈ R3 is Euler angle in inertial coordinate, T and τ are the total force and moment act on the frame of NQRs, ez=[0, 0, 1]T is a vector along Ez, and I =diag(Ix, Iy, Iz) is the moment of inertial matrix.The rotation matrix R (Θ), which transforms a vector from inertial coordinate to body coordinate, has an expression as
| $ \mathit{\boldsymbol{R}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \varphi \sin \psi + \sin \varphi \cos \psi }&{\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi }\\ {\cos \theta \cos \psi }&{\cos \varphi \sin \psi + \sin \varphi \cos \psi }&{ - \sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi }\\ { - \sin \theta }&{\sin \varphi \cos \theta }&{\cos \varphi \cos \theta } \end{array}} \right] $ |
And the attitude kinematic matrix K(Θ) is defined as
| $ \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta }\\ 0&{\cos \varphi }&{ - \sin \varphi }\\ 0&{\sin \varphi \sec \theta }&{\cos \varphi \sec \theta } \end{array}} \right] $ |
During the flight, NQRs may be influenced by internal and external uncertainties, for example, the vibration derives from the asymmetry of eccentricity of rotor shafts, asymmetry of rotor blades and asymmetry of frame, winds and gusts and so forth. Hence, taking consideration of uncertainties, Eq.(2) yields the altitude and attitude movement equations of NQRs, shown as
| $ \left\{ \begin{array}{l} \ddot h = - g + \frac{{{T_r} + \Delta {T_r}}}{m}\cos \varphi \cos \theta \\ \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }} = \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)\mathit{\boldsymbol{\omega }}\\ \mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{f}}_{pqr}} + \mathit{\boldsymbol{V}} \end{array} \right. $ | (2) |
where
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{pqr}} = \left[ {\begin{array}{*{20}{c}} {{f_p}}\\ {{f_q}}\\ {{f_r}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{I_y} - {I_z}}}{{{I_x}}}qr}\\ {\frac{{{I_z} - {I_x}}}{{{I_y}}}pr}\\ {\frac{{{I_z} - {I_x}}}{{{I_z}}}pq} \end{array}} \right] + }\\ {\left[ {\begin{array}{*{20}{c}} {\frac{l}{{{I_x}}}}&0&0\\ 0&{\frac{l}{{{I_y}}}}&0\\ 0&0&{\frac{l}{{{I_z}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\tau _{{\rm{roll}}}}}\\ {\Delta {\tau _{{\rm{pitch}}}}}\\ {\Delta {\tau _{{\rm{yaw}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\Delta {d_{{\rm{roll}}}}}\\ {\Delta {d_{{\rm{pitch}}}}}\\ {\Delta {d_{{\rm{yaw}}}}} \end{array}} \right]} \end{array} $ | (3) |
| $ \mathit{\boldsymbol{V = }}\left[ {\begin{array}{*{20}{c}} {{V_1}}\\ {{V_2}}\\ {{V_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{l}{{{I_x}}}}&0&0\\ 0&{\frac{l}{{{I_y}}}}&0\\ 0&0&{\frac{l}{{{I_z}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta {\tau _{{\rm{roll}}}}}\\ {\Delta {\tau _{{\rm{pitch}}}}}\\ {\Delta {\tau _{{\rm{yaw}}}}} \end{array}} \right] $ | (4) |
In Eq.(4), [Δτroll, Δτpitch, Δτyaw]T represents the movement disturbances and [Δdroll, Δdpitch, Δdyaw]T represents the internal uncertainties.
2 Brief Introduction of LESO 2.1 Fundamental theory of high-order LESOThe (n+1) th-order LESO is mainly used to observe nth-ordercontrolsystem. Take the following nth-order linear affine differential system as an example
| $ \Sigma :\left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ \; \vdots \\ {{\dot x}_n} = f\left( {{x_1}, \cdots ,{x_n},t} \right) + b \cdot u\\ y = {x_1} \end{array} \right. $ | (5) |
where u and y are input and output of Σ, respectively, and b > 0. Assume that f(x1, …, xn, t) is bounded and differentiable and its derivative with respect to t is n(x1, …, xn, t). Also bounded, this assumption is always reasonable in the control of quad-rotors. Then system Σ can be extended as the following formation
| $ {\Sigma _{{\rm{extend}}}}:\left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ \; \vdots \\ {{\dot x}_n} = {x_{n + 1}} + b \cdot u\\ {{\dot x}_{n + 1}} = n\left( {{x_1}, \cdots ,{x_n},t} \right)\\ y = {x_1} \end{array} \right. $ | (6) |
Using a linear state observer[19-21] to observe Σextend yields
| $ {\Sigma _{{\rm{ESO}}}}:\left\{ \begin{array}{l} e = {z_1} - y\\ {{\dot z}_1} = {z_2} - {\sigma _1} \cdot e\\ \; \vdots \\ {{\dot z}_n} = {z_{n + 1}} - {\sigma _n} \cdot e + b \cdot u\\ {{\dot z}_{n + 1}} = - {\sigma _{n + 1}} \cdot e\\ y = {x_1} \end{array} \right. $ | (7) |
The above system ΣESO is the so-called LESO. Thus, zi tracks xi(i=1, …, n) and zn+1 estimates f(x1, …, xn, t).
2.2 Stability analysis of LESOIn this part, stability of the (n+1) th-order LESO is proved. Firstly, rewrite Eq.(7) as the following formation
| $ \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{B}}_u} \cdot u + {\mathit{\boldsymbol{B}}_n} \cdot n $ | (8) |
where
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = {{\left[ {{x_1}, \cdots ,{x_n}} \right]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&0& \cdots &0&0\\ 0&0&1& \cdots &0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ 0&0&0& \cdots &0&1\\ 0&0&0& \cdots &0&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{B}}_u} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ b\\ 0 \end{array}} \right],{\mathit{\boldsymbol{B}}_n} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ 0\\ 1 \end{array}} \right]} \end{array} $ | (9) |
AndEq.(8) can be rewritten as
| $ \mathit{\boldsymbol{\dot Z}} = \mathit{\boldsymbol{A}} \cdot \mathit{\boldsymbol{Z}} + {\mathit{\boldsymbol{B}}_u} \cdot u + {\mathit{\boldsymbol{B}}_E} \cdot \mathit{\boldsymbol{E}} $ | (10) |
where
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}} = {{\left[ {{z_1}, \cdots ,{z_{n + 1}}} \right]}^{\rm{T}}},{\mathit{\boldsymbol{e}}_i} = {z_i} - {x_i}\;\;\;i = 1, \cdots ,n + 1}\\ {\mathit{\boldsymbol{E}} = {{\left[ {{\mathit{\boldsymbol{e}}_1},{\mathit{\boldsymbol{e}}_2}, \cdots ,{\mathit{\boldsymbol{e}}_n},{\mathit{\boldsymbol{e}}_{n + 1}}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{B}}_E} = \left[ {\begin{array}{*{20}{c}} { - {\sigma _1}}&0&0& \cdots &0&0\\ { - {\sigma _2}}&0&0& \cdots &0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ { - {\sigma _n}}&0&0& \cdots &0&0\\ { - {\sigma _{n + 1}}}&0&0& \cdots &0&0 \end{array}} \right]} \end{array} $ | (11) |
Hence, subtracting Eq.(9) from Eq.(11) yields
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot E}} = {\mathit{\boldsymbol{A}}_E} \cdot \mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{B}}_n} \cdot n = }\\ {\left[ {\begin{array}{*{20}{c}} { - {\sigma _1}}&1&0& \cdots &0&0\\ { - {\sigma _2}}&0&1& \cdots &0&0\\ \vdots&\vdots&\vdots&\ddots&\vdots&\vdots \\ { - {\sigma _n}}&0&0& \cdots &0&1\\ { - {\sigma _{n + 1}}}&0&0& \cdots &0&0 \end{array}} \right] \cdot \mathit{\boldsymbol{E}} - \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ \vdots \\ 0\\ 1 \end{array}} \right] \cdot n} \end{array} $ | (12) |
Since n=n(x1, …, xn, t) is a bounded function as defined before, the (n+1)th-order LESO is bounded-input bounded-output (BIBO) if the roots of the characteristic polynomial of AE, shown as
| $ \lambda \left( p \right) = {p^{n + 1}} + {\sigma _1}{p^n} + {\sigma _2}{p^{n - 1}} + \cdots + {\sigma _n}p + {\sigma _{n + 1}} $ | (13) |
are all in the left half plane. Thus, stability of the (n+1) th-order LESO is proved.
3 Design of Altitude Control Law 3.1 Design of NDI-based altitude control lawIn this part, an altitude control law based on NDI is derived. During the motion of NQR, cosφ≈1, cosθ≈1 and ΔTr is uncertain. Hence, in NDI, Eq.(2) is usually rewritten as
| $ \ddot h = - g + \frac{{{T_r}}}{m} $ | (14) |
Denoting fz=-g and
| $ \ddot h = {f_z} + {g_z} \cdot {T_r} $ | (15) |
Solving the above equation yields the desired thrust, that is
| $ {T_{rd}} = g_z^{ - 1} \cdot \left( {\ddot h - {f_z}} \right) $ | (16) |
where
Assume that hd represents the desired trajectory of altitude and h represents the feedback trajectory of altitude, then the tracking error e=hd-h satisfies the following equation
| $ \ddot e + {k_d}\dot e + {k_p}e = 0 $ |
Therefore, by substituting e=hd-h into the above equation, expression of
| $ \ddot h = {{\ddot h}_d} + {k_d}\left( {{{\dot h}_d} - \dot h} \right) + {k_p}\left( {{h_d} - h} \right) $ |
According to the above analysis, the overall structure of the altitude control system based on NDI is shown in Fig. 2.
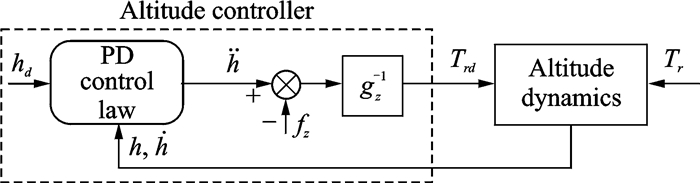
|
Fig. 2 Structure of the altitude control system based on NDI for NQRs |
3.2 INDI-based altitude control law improved using LESO
In NDI, ΔTr is ignored, which always results in the low accuracy of the counteraction of nonlinear terms since ΔTr usually affects the quality of the controller and the robustness of the system. In this part, ΔTr is taken into account by taking advantage of LESO.In Eq.(16), considering the disturbance ΔTr and putting it into fz yields
| $ \left\{ \begin{array}{l} \ddot h = {{\bar f}_z} + {g_z} \cdot {T_r}\\ {{\bar f}_z} = - g + \frac{{\Delta {T_r}}}{m} \end{array} \right. $ | (17) |
By denoting x1=h, x2=
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {x_3} + {g_z} \cdot {T_r}\\ {{\dot x}_3} = {n_z}\\ y = {x_1} \end{array} \right. $ | (18) |
Using third-order LESO to observe the above extended system yields
| $ \left\{ \begin{array}{l} e = y - {z_1}\\ {{\dot z}_1} = {z_2} - {\rho _1} \cdot e\\ {{\dot z}_2} = {z_3} - {\rho _2} \cdot e + {g_z} \cdot {T_r}\\ {{\dot z}_3} = - {\rho _3} \cdot e \end{array} \right. $ | (19) |
Therefore, z1 tracks x1, z2 tracks x2, and z3 estimates fz.
By using LESO to make the estimation, the control scheme changes into the following pattern, as shown in Fig. 3.
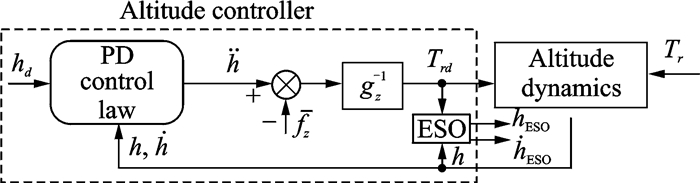
|
Fig. 3 Structure of the INDI-based altitude control system improved using LESO for NQRs |
A direct method to verify the correctness of this theory is to check the agreement between
On one hand, in Eq.(18), following the relationship between kd and kp can ensure the disappearance of overshoot
| $ {k_p} = {\lambda ^2},{k_d} = 2\lambda \;\;\;\lambda > 0 $ | (20) |
On the other hand, to derive the parameters of the third-order LESO, transfer function of Eq.(22) from z3 to y and Tr needs to be obtained, shown as
| $ {z_3} = \frac{{\rho _3^z}}{{{s^3} + \rho _1^z \cdot {s^2} + \rho _2^z \cdot s + \rho _3^z}}\left( {{s^2} \cdot y - {g_z} \cdot {T_r}} \right) $ | (21) |
According to Ref.[22], ρ1z, ρ2z and ρ3z can be determined as
| $ \rho _1^z = 3{\omega _z},\rho _2^z = 3\omega _z^2,\rho _3^z = \omega _z^3\;\;\;{\omega _z} > 0 $ | (22) |
where ωz is called bandwidth of roll angular velocity channel and thus the transfer function turns into
| $ {z_3} = \frac{{\omega _z^3}}{{{{\left( {s + {\omega _z}} \right)}^3}}}\left( {{s^2} \cdot y - {g_z} \cdot {T_r}} \right) $ | (23) |
Therefore, in the altitude control system, only one parameter needs to be tuned since λ can be determined empirically, for example, its recommended value can be 1 or 2.
4 Designof Attitude Control Law 4.1 Design of NDI-based attitude control lawTo derive the Euler angle control law, Eq.(2) needs to be addressed.
Denote
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta }\\ 0&{\cos \varphi }&{ - \sin \varphi }\\ 0&{\sin \varphi \sec \theta }&{\cos \varphi \sec \theta } \end{array}} \right] $ | (24) |
Hence, Eq.(2) can be rewritten as
| $ {\left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right]_d} = \mathit{\boldsymbol{T}}{\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right]_d} $ | (25) |
Then the desired angular velocity and the input of angular velocity controller can be obtained as
| $ {\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right]_d} = {\mathit{\boldsymbol{T}}^{ - 1}}{\left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right]_d} $ | (26) |
where
| $ {\left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot \theta }\\ {\dot \psi } \end{array}} \right]_d} = {\mathit{\boldsymbol{K}}_1}\left\{ {{{\left[ {\begin{array}{*{20}{c}} \varphi \\ \theta \\ \psi \end{array}} \right]}_d} - \left[ {\begin{array}{*{20}{c}} \varphi \\ \theta \\ \psi \end{array}} \right]} \right\} $ | (27) |
and [φ, θ, ψ]T is the real-time feedback value of attitude and K1= diag (ω1, ω1, ω1).
After deriving the Euler angle controller, the angular velocity controller needs to be designed.
In Eqs.(4), (5), denote
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {\frac{l}{{{I_x}}}}&0&0\\ 0&{\frac{l}{{{I_y}}}}&0\\ 0&0&{\frac{l}{{{I_z}}}} \end{array}} \right] $ | (28) |
And rewrite Eq.(4) as
| $ {\left[ {\begin{array}{*{20}{c}} {\dot p}\\ {\dot q}\\ {\dot r} \end{array}} \right]_d} = \left[ {\begin{array}{*{20}{c}} {{f_p}}\\ {{f_q}}\\ {{f_r}} \end{array}} \right] + \mathit{\boldsymbol{R}}{\left[ {\begin{array}{*{20}{c}} {{\tau _{{\rm{roll}}}}}\\ {{\tau _{{\rm{pitch}}}}}\\ {{\tau _{{\rm{yaw}}}}} \end{array}} \right]_d} $ | (29) |
Then the desired virtual input can be solved, shown as
| $ {\left[ {\begin{array}{*{20}{c}} {{\tau _{{\rm{roll}}}}}\\ {{\tau _{{\rm{pitch}}}}}\\ {{\tau _{{\rm{yaw}}}}} \end{array}} \right]_d} = {\mathit{\boldsymbol{R}}^{ - 1}}\left\{ {{{\left[ {\begin{array}{*{20}{c}} {\dot p}\\ {\dot q}\\ {\dot r} \end{array}} \right]}_d} - \left[ {\begin{array}{*{20}{c}} {{f_p}}\\ {{f_q}}\\ {{f_r}} \end{array}} \right]} \right\} $ | (30) |
where
| $ {\left[ {\begin{array}{*{20}{c}} {\dot p}\\ {\dot q}\\ {\dot r} \end{array}} \right]_d} = {\mathit{\boldsymbol{K}}_2}\left\{ {{{\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right]}_d} - \left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right]} \right\} $ | (31) |
The desired angular velocity [p, q, r]dT has been obtained in above [p, q, r]T is the real-time feedback value of angular velocity, and K2= diag (ω2, ω2, ω2).
According to the above analysis, the overall structure of the attitude control system is shown in Fig. 4.

|
Fig. 4 Structure of the NDI-based attitude control system for NQRs |
The above analysis also clearly shows the biggest weakness of TNDI, that is, the robustness and quality of the attitude controller depends on the modeling precision of [fp, fq, fr]T. Ref.[19] has proved that TNDI can address the case with small perturbations in [fp, fq, fr]T; while with large perturbations in [fp, fq, fr]T, for instance, in the existence of persistent external uncertainties, the TNDI cannot perform well. In most cases, the nonlinearity of the model can be counteracted completely only when the nonlinear terms [fp, fq, fr]T are accurate enough, which restrains the application of TNDI.
4.2 INDI-based attitude control law improved using LESOTo overcome the weakness discussed above, LESO is used to estimate the accurate and real time value of [fp, fq, fr]T. Hence, it is necessary to introduce the LESO first and then give the improved control law based on LESO. In this paper, only the estimation of fp using LESO is introduced as fq and fr are very similar.
In the first equation of Eq.(2), denote that
| $ \left\{ \begin{array}{l} {x_1} = p\\ {x_2} = {f_p}\\ {{\dot x}_2} = {g_p} \end{array} \right. $ | (32) |
Hence, the roll angular velocity system is rewritten as
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2} + \frac{l}{{{I_x}}} \cdot {\tau _{{\rm{roll}}}}\\ {{\dot x}_2} = {g_p}\\ y = {x_1} \end{array} \right. $ | (33) |
Using second-order LESO to observe the above extended system yields
| $ \left\{ \begin{array}{l} e = y - {z_1}\\ {{\dot z}_1} = {z_2} - \rho _1^p \cdot e + \frac{l}{{{I_x}}} \cdot {\tau _{{\rm{roll}}}}\\ {{\dot z}_2} = - \rho _2^p \cdot e \end{array} \right. $ | (34) |
Therefore, z1 tracks p and z2 estimates fp.
By employingLESO to conduct the estimation, the control scheme changes into the following pattern, as shown in Fig. 5.
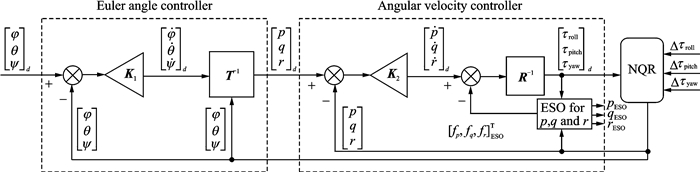
|
Fig. 5 Structure of the INDI-based attitude control system using LESOforNQRs |
A direct method to verify the correctness of this theory is to check the agreement between [p, q, r]T and [pESO, qESO, rESO]T, which will be checked in simulations hereinafter.
4.3 Parameter tuning principles of attitude controlIn one way, in the attitude controller, the parameters ω1 and ω2 together determine both the tracking precision and the response speed of the system. Since the response speed of angular velocity is much faster than the one of Euler angle, thus, the two parameters usually satisfy the following relationship[19]
| $ {\omega _2} = n \cdot {\omega _1}\;\;\;\;n = 3 - 5 $ | (35) |
Put another way, in the LESO, ρ1p and ρ2p determine the tracking precision and speed, too small value may cause a bad tracking performance and too large value may result in divergence of the system. Taking the transfer function of Eq.(34) yields
| $ {z_2} = \frac{{\rho _2^p}}{{{s^2} + \rho _1^p \cdot s + \rho _2^p}}\left( {s \cdot y - \frac{l}{{{I_x}}} \cdot {\tau _{{\rm{roll}}}}} \right) $ | (36) |
Notice that it is a typical second order system and to avoid the overshoot, Gao[22] also recommended a method to determine ρ1p and ρ2p, shown as
| $ \rho _1^p = 2{\omega _p},\rho _2^p = \omega _p^2\;\;\;\;{\omega _p} > 0 $ | (37) |
where ωp is called bandwidth of roll angular velocity channel and thus, the transfer function turns into
| $ {z_2} = \frac{{\omega _p^2}}{{{{\left( {s + {\omega _p}} \right)}^2}}}\left( {s \cdot y - \frac{l}{{{I_x}}} \cdot {\tau _{{\rm{roll}}}}} \right) $ | (38) |
Hence, in each angular velocity channel (roll, pitch and yaw), only two parameters need to be determined.
5 Numerical ValidationTwo numerical simulations were conducted.The first one aims to demonstrate the superiority of INDI compared with TNDI in the existence of model uncertainties; and the second one in turn demonstrates the superiority of INDI compared with TNDI in the existence of both external uncertainties and model uncertainties.
5.1 Variables and parametersThe parameters of the NQR used in the simulations are listed in Table 1.
| Table 1 Parameters of NQR |
The initial conditions are given as
| $ \left\{ \begin{array}{l} {h_0} = 0\\ \left( {\varphi ,\theta ,\psi } \right)_0^{\rm{T}} = {\left( {0,0,0} \right)^{\rm{T}}}\\ \left( {p,q,r} \right)_0^{\rm{T}} = {\left( {0,0,0} \right)^{\rm{T}}} \end{array} \right. $ | (39) |
The desired altitude and attitude trajectories are given as
| $ \left\{ \begin{array}{l} {h_d}\left( t \right) = 4 + 3\sin t\left( m \right)\\ {\left[ {{\varphi _d},{\theta _d},{\psi _d}} \right]^{\rm{T}}} = {\left[ {0.1\;{\rm{rad}},0.1\;{\rm{rad}},0.1\;{\rm{rad}}} \right]^{\rm{T}}} \end{array} \right. $ | (40) |
Values of parameters of NDI controllers are shown in Table 2. Values of parameters of LESOs are shown in Table 3.
| Table 2 Values of parameters of NDI controllers |
| Table 3 Values of parameters of LESOs |
5.2 Case study: INDI vs. TNDI under low and high frequency uncertainties
In this part, low and high frequency uncertainties were considered together. Δdroll, Δdpitch and Δdyaw were assumed to be the triangle functions including low and high frequency components. This assumption is reasonable since such uncertainties derive from many aspects, for instance, eccentricity of rotor shafts, asymmetry of both rotor blades and frame, body vibration on sensors, unstable voltage of circuit and larger ripple current, and they can be modeled and extended to the trigonometric series.Furthermore, there was an additional mass (8% of the mass of NQR) added on the NQR during its flight meanwhile. The figures of state variables and outputs of NQR are shown in Figs. 6-21.

|
Fig. 6 Response of altitude |
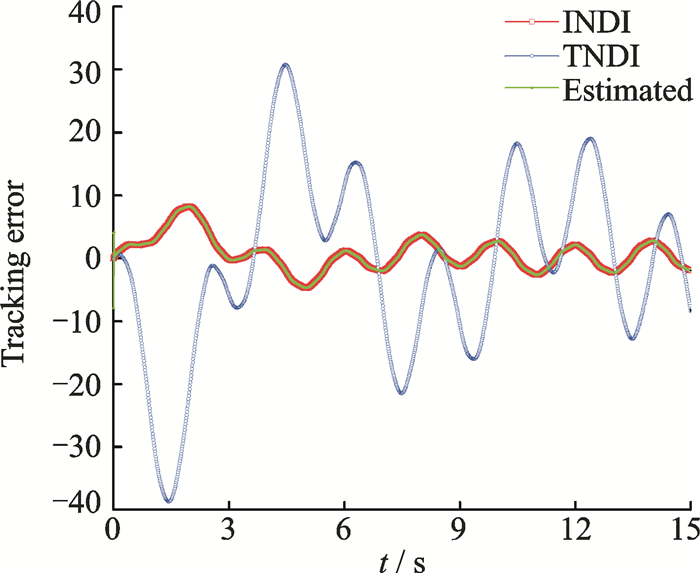
|
Fig. 7 Tracking error of altitude response |
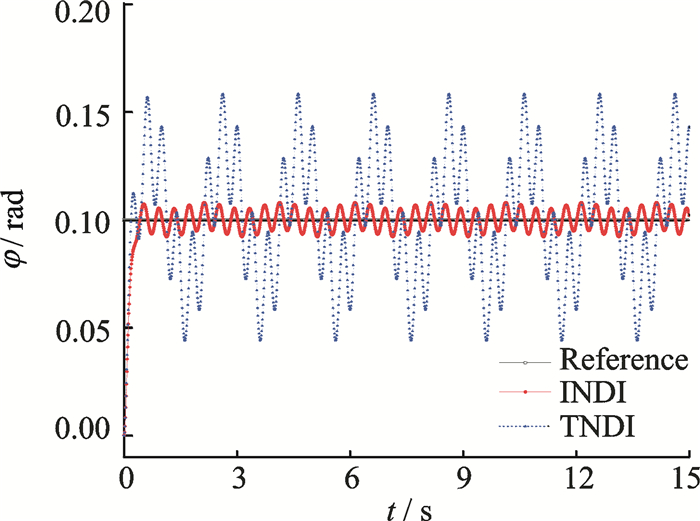
|
Fig. 8 Response of roll angle |
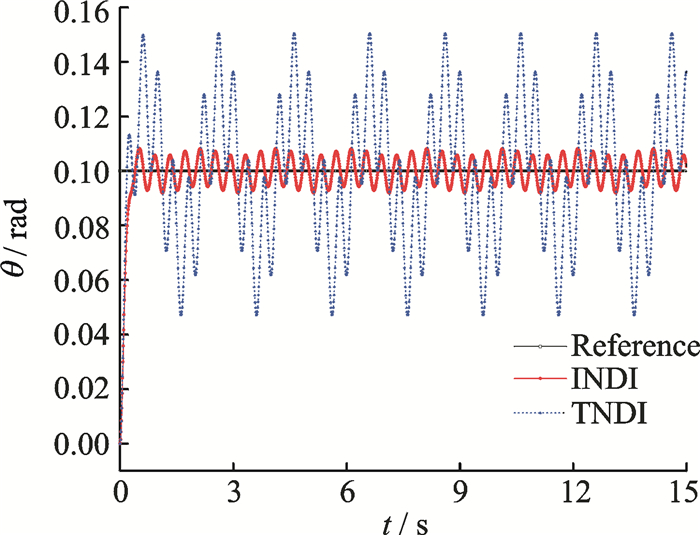
|
Fig. 9 Response of pitch angle |
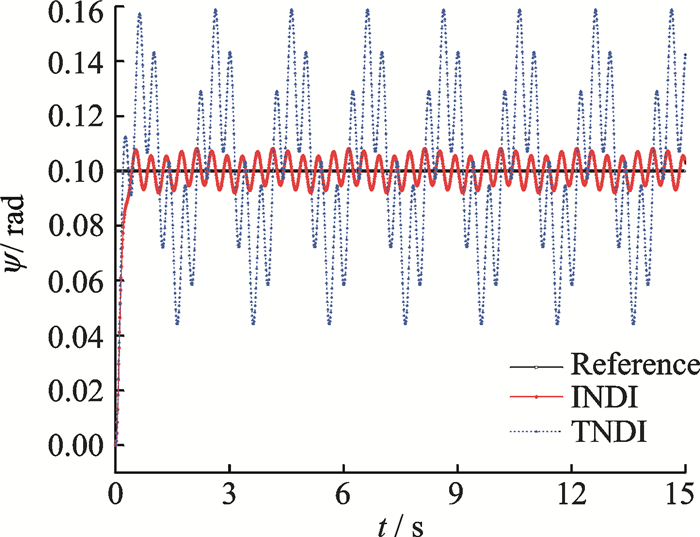
|
Fig. 10 Response of yaw angle |
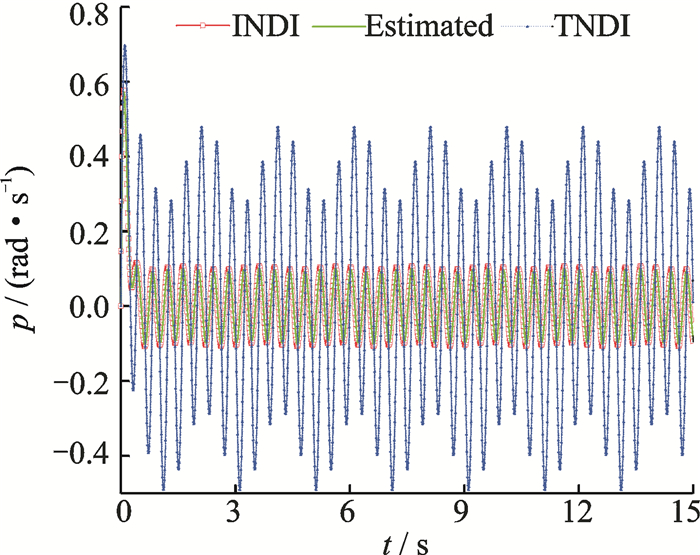
|
Fig. 11 Roll angular rate |
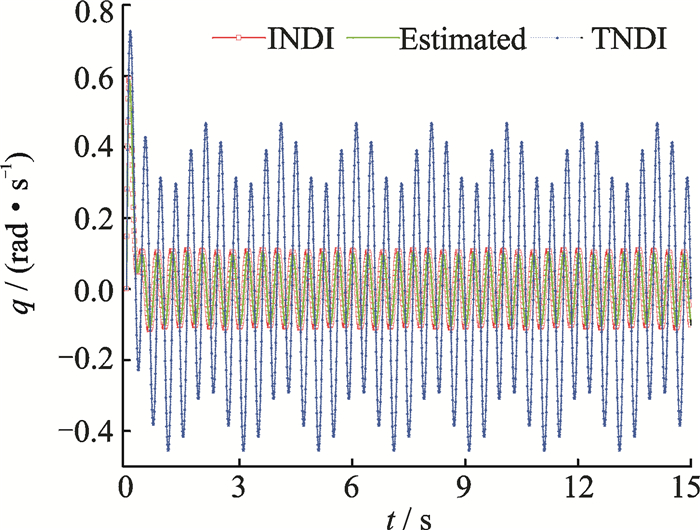
|
Fig. 12 Pitch angular rate |
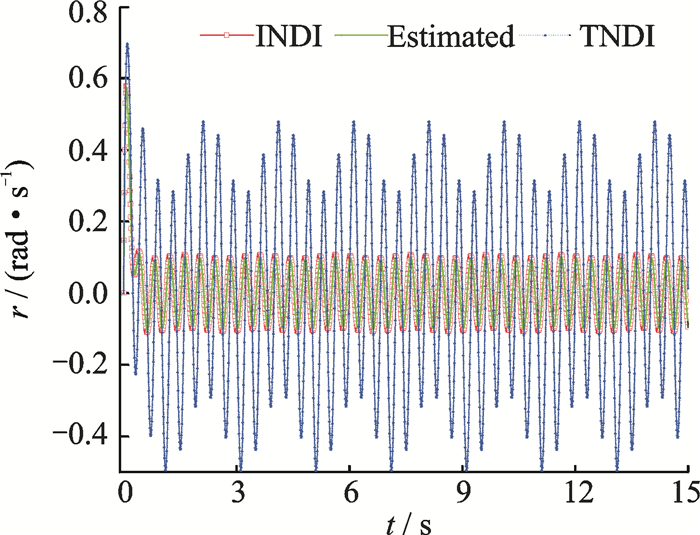
|
Fig. 13 Yaw angular rate |
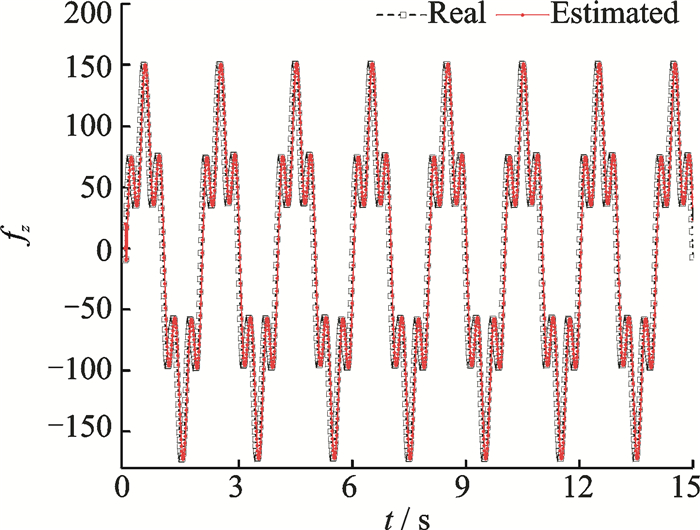
|
Fig. 14 Estimation of fz by LESO |
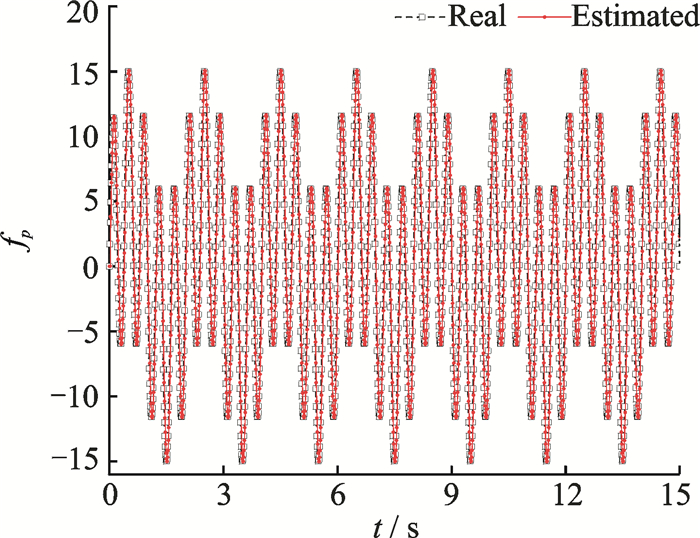
|
Fig. 15 Estimation of fp by LESO |
|
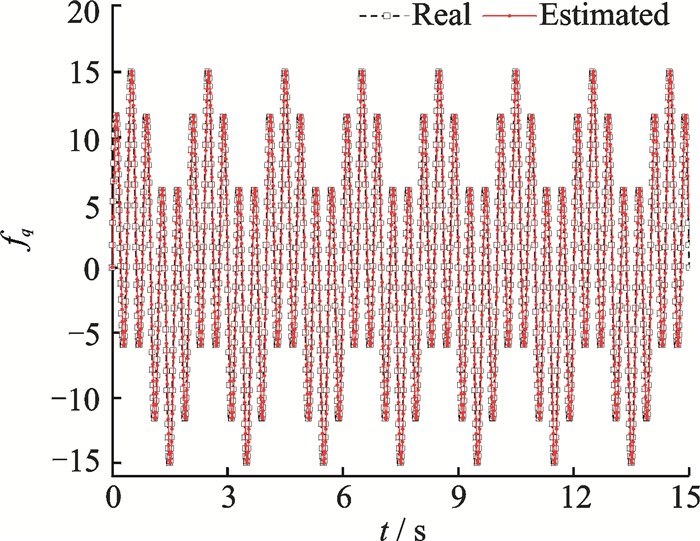
Fig. 16 Estimation of fq by LESO |
|
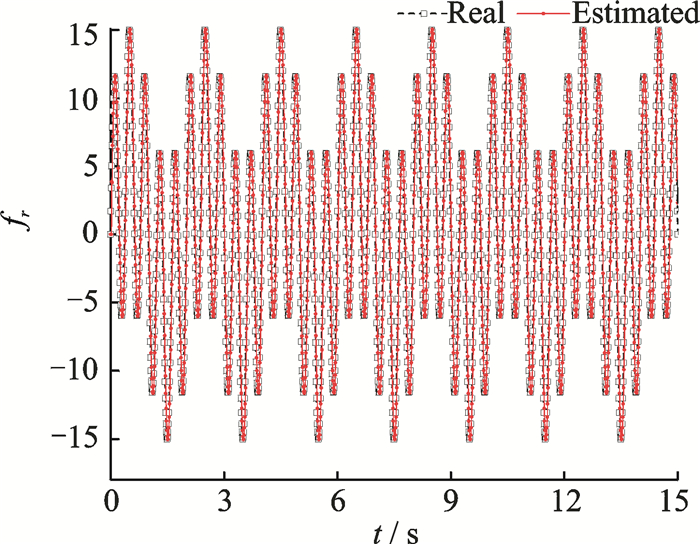
Fig. 17 Estimation of fr by LESO |
|
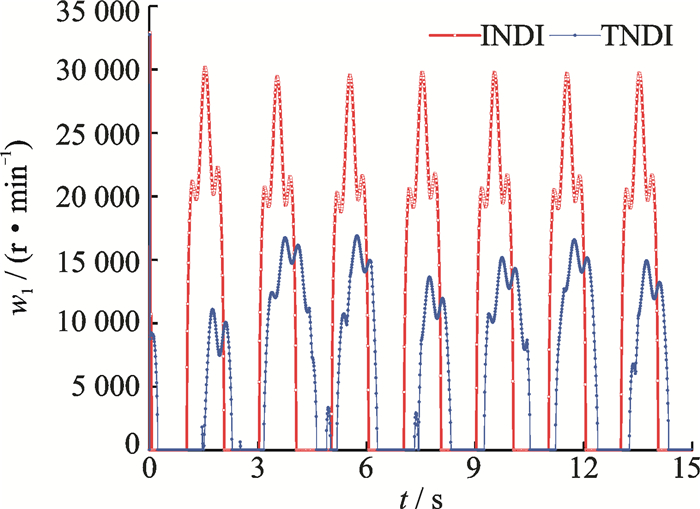
Fig. 18 Speed of rotor 1 |
|
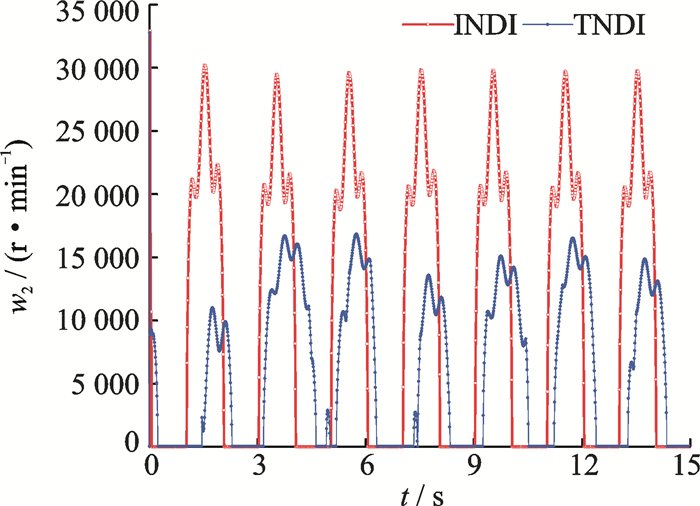
Fig. 19 Speed of rotor 2 |
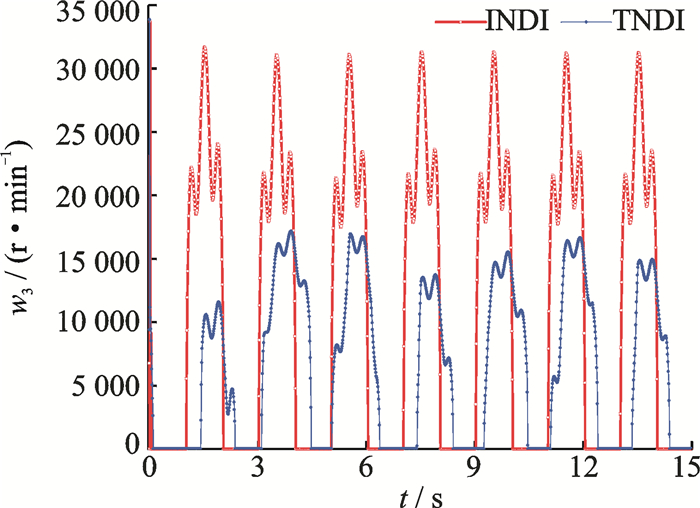
|
Fig. 20 Speed of rotor 3 |
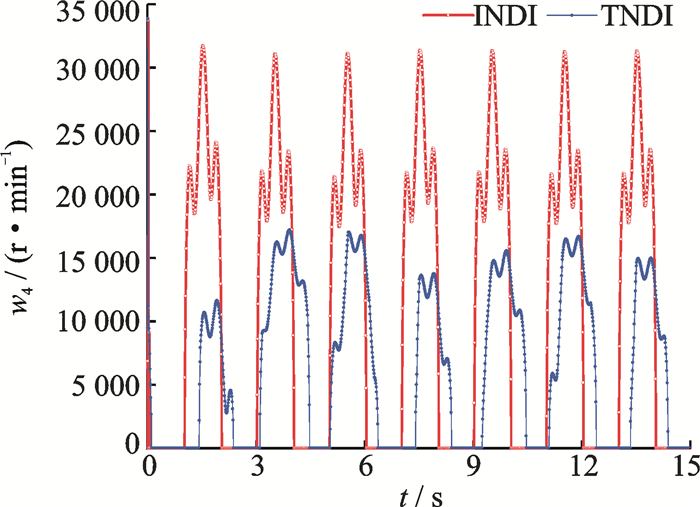
|
Fig. 21 Speed of rotor 4 |
Fig. 6, Fig. 7 and Fig. 14 show the simulation results in altitude control using the INDI-based and TNDI-based methods. Fig. 6 and Fig. 7 together depict the tracking results, and obviously the tracking effect derived from the INDI-based method is much better (also acceptable) than the one from the TNDI-based method since the former one owns much higher accuracy.The correctness of the estimation obtained by LESO is also demonstrated in the three figures since the curves of the estimated state variables are overlapped with the ones of the real state variables.
Figs. 8-10 show the results in attitude control using both methods. It is clear that the INDI-based method can still hold the attitude of the NQR steady even under persistent high/low frequency disturbances.
Figs. 18-21 show the desired rotor speed of the NQR. Notice that the curves of the input variables in the TNDI-based method are much smoother than those in the INDI-based method. The reason is that, in TNDI uncertainties rejection mostly relies on the robustness of its controller. When uncertainties are added into the plant, the controller cannot make response to them, which results in the smooth curves. While situations are different in the INDI-based method since LESO has the ability to estimate uncertainties, and then counteract them in each time step, which results in the fluctuation of the curves of the input variables in INDI-based method. This also in turn explains why the INDI-based method has better tracking precision in both altitude and attitude controls.
6 ConclusionsAn INDI-based method is developed to design the altitude and attitude control systems for NQRs. To solve the problem that TNDI relies heavily on accurate model of NQR, which is difficult to be obtained, and to retain the robustness of TNDI, the LESO is introduced into TNDI to estimate the model and external uncertainties and then counteract in real time. Comparison between simulation results of the two methods shows that the INDI-based method can reject the uncertainties better, and it does not rely on the accurate model, presenting significant superiority.
Acknowledgements
This work was supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) and the Advanced Research Project of Army Equipment Development (No.301020803).
| [1] |
SÁ R C, ARAÚJO A L, VARELA A T, et al. Construction and PID control for stability of an unmanned aerial vehicle of the type quadrotor[J]. Robotics Symposium and Competition, 2013, 10: 95-99. |
| [2] |
BOUABDALLAH S, NOTH A, SIEGWART R. PID vs LQ control techniques applied to an indoor microquadrotor[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Sendai, Japan: IEEE, 2004, 3: 2451-2456.
|
| [3] |
BOUABDALLAH S, SIEGWART R. Design and control of a miniature quadrotor[C]//Advances in Unmanned Aerial Vehicles. Netherlands: Springer, 2007, 33: 171-210.
|
| [4] |
DIERKS T, JAGANNATHAN S. Output feedback control of a quadrotoruav using neural networks[J]. IEEE Transactions on Neural Networks, 2010, 21(1): 50-66. DOI:10.1109/TNN.2009.2034145 |
| [5] |
VOOS H. Nonlinear control of a quadrotor micro-UAV using feedback-linearization[C]//IEEE International Conference on Mechatronics. [S.l.]: IEEE, 2009: 1-6.
|
| [6] |
HUA M D, HAMEL T, MORIN P, et al. A control approach for thrust-propelled underactuated vehicles and its application to VTOL drones[J]. IEEE Transactions on Automatic Control, 2009, 54(8): 1837-1853. DOI:10.1109/TAC.2009.2024569 |
| [7] |
DIKMEN I C, ARISOY A, TEMELTAS H. Attitude control of a quadrotor[C]//International Conference on Recent Advances in Space Technologies. Istanbul, Turkey: IEEE, 2009: 722-727.
|
| [8] |
TIWARI S, PADHI R. DR-SNAC aided dynamic inversion controller for robust trajectory tracking of a micro-quadrotor[C]//AIAA Guidance, Navigation, and Control. Boston, MA: IEEE, 2013: 1-28.
|
| [9] |
XU Y, TONG C, LI H. Flight control of a quadrotor under model uncertainties[J]. International Journal of Micro Air Vehicles, 2015, 7(1): 1-20. DOI:10.1260/1756-8293.7.1.1 |
| [10] |
ZHAO B, XIAN B, ZHANG Y, et al. Nonlinear robust adaptive tracking control of a quadrotoruav via immersion and invariance methodology[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2891-2902. DOI:10.1109/TIE.2014.2364982 |
| [11] |
MADANI T, BENALLEGUE A. Control of a quadrotor mini-helicopter via full state Backstepping technique[C]//Proceedings of the IEEE Conference on Decision and Control. [S.l.]: IEEE, 2006: 1515-1520.
|
| [12] |
KHEBBACHE H, TADJINE M. Robust fuzzy Backstepping sliding mode controller for a quadrotor unmanned aerial vehicle[J]. Control Engineering & Applied Informatics, 2013, 15(2): 3-11. |
| [13] |
LEE D, LIM H, KIM H J, et al. Adaptive image-based visual serving for an underactuatedquadrotorsystem[J]. Journal of Guidance Control & Dynamics, 2012, 35(4): 1335-1353. |
| [14] |
KUN D W, HWANG I. Linear matrix inequality-based nonlinear adaptive robust control of quadrotor[J]. Journal of Guidance Control & Dynamics, 2015, 1-13. |
| [15] |
BESNARD L, SHTESSEL Y B, Landrum B. Quadrotor vehicle control via sliding mode controller driven by sliding mode disturbance observer[J]. Journal of the Franklin Institute, 2012, 349(2): 658-684. DOI:10.1016/j.jfranklin.2011.06.031 |
| [16] |
ALEXIS K, NIKOLAKOPOULOS G, TZES A. Constrained-control of a quadrotor helicopter for trajectory tracking under wind-gust disturbances[C]//IEEE Mediterranean Electrotechnical Conference. Valletta, Malta: IEEE, 2010: 1411-1416.
|
| [17] |
MUÑOZ L E, CASTILLO P, SANAHUJA G, et al. Embedded robust nonlinear control for a four-rotor rotorcraft: Validation in real-time with wind disturbances[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco, CA, USA: IEEE, 2011: 2682-2687.
|
| [18] |
ITO D, GEORGIE J, VALASEK J, et al. Reentry vehicle flight controls design guidelines: Dynamic inversion[R]. NASA/TP 2002-210771, 2002.
|
| [19] |
DOU J, KONG X, WEN B. Altitude and attitude active disturbance rejection controller design of a quadrotor unmanned aerial vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2016. DOI:10.1177/0954410016660871 |
| [20] |
HAN J. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [21] |
HAN J Q. Active disturbance rejection control technique the technique for estimating and compensating the uncertainties. 1st ed[M]. Beijing: National Defense Industry Press, 2008.
|
| [22] |
GAO Z. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference. Denver, CO, USA: IEEE, 2003, 6: 4989-4996.
|
 2018, Vol. 35
2018, Vol. 35


