In recent years, carbon fiber reinforced plastic (CFRP) has wide applications in fields of aeronautics and astronautics. Compared with aluminum alloy, CFRP parts are able to stand equal load with relative lower density, which decreases the whole weight[1-2]. Among several composite manufacturing technologies, automated fiber placement(AFP) and automated tape laying(ATL) have been increasingly applicated in various fields. Automation and high efficiency are the main advantages over traditional techniques.
The essential difference between AFP and ATL is the width of the prepreg. In general, AFP uses narrow tows (1/8″ to 1/2″) while ATL uses large scale tape (up to 300 mm). Thus, according to prepreg width, ATL is capable of processing part of small curvature or plate in high efficiency while complex parts with sharp curvature variation are the option of AFP[3]. AFP and ATL both place prepreg on the mould surface to generate a part. During the placement process, an elastic roll is used to press the heated prepreg on the mould surface to make the ply compact. Based on the designed placement angle, tool path is generated to guide end-effector to conduct placement process, which requires the surface covered without gap or overlap between adjacent tapes or groups of tows[4]. In terms of AFP, it places various tows simultaneously and each tow is driven individually and can be clamped, cut, and restarted during manufacturing. This makes it possible to deliver each tow at individual speed, enabling some tow steerings to fit various path design. However, fiber steer causes manufacturing defects and it results from the material property. According to fiber steer, part is produced in optimal mechanics design but the defects such as buckling and bridging would damage the product quality[5].
CAD/CAM software technology is crucial to AFP, and it computes accurate tool path and is transfered into NC code for manufacturing. Besides proposing new tool path generating method, post-process of already computed tool path is another research emphasis[6-7].
Based on an already computed path, post-fairing method is able to optimize the current path.Fleisig et al.[8] fitted 5-axis tool path in three B-spline, which focused on the reduction of processing time. Ho et al.[9] proposed a quaternion method to smooth the tool orientation under permitted error range. Taking advantage of the degree of tool machine redundancy, Piece et al.[10] improved the AFP tool kinematic behavior and decreased the processing time. Above all, the studies on tool path smoothing mainly concentrate on reducing processing time and improving tool kinematic behavior, while tool path position fairing in AFP is not mentioned. Layup quality is sensitive to path curvature because of the material inherent property. When the geodesic curvature of tool path reaches its critical value, bulking defect takes place and it may lead to part quality decrease or even placement failure. We propose a post-fairing approach that dedicates to improve AFP path smoothness for better product quality.
1 AFP Tool Path Analysis 1.1 Placement steering analysisPrepreg typically consists of reinforcement fiber and resin matrix. It is expected that prepreg tows are placed onto the mold with winkle. However, in case of large curvature part, it is inevitable to produce defects, e. g. buckling. The detailed analysis is as follows:
As shown in Fig. 1, the curvature k of surface curve can be decomposed into kn and kg, which represent the direction of n (which is the surface normal) and u (which is normal to n and the tangent t), respectively. It is illustrated as: u=t×n. Then, curvature k is decomposed as
| $ k = {k_g} + {k_n} $ | (1) |
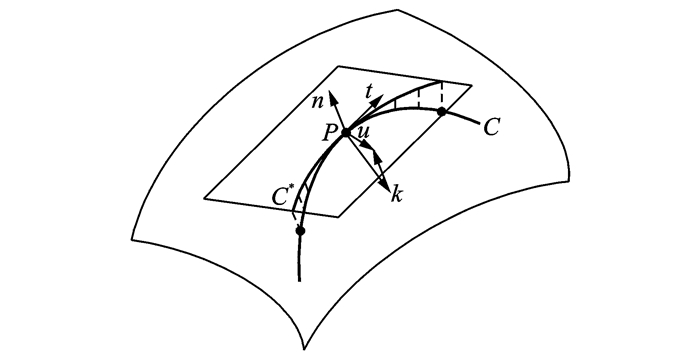
|
Fig. 1 Frame coordinate of surface curve |
Tool path in AFP represents the central line of tows. n and u represent the thickness direction and the width direction of prepreg, respectively. According to the bent beam theory, in case of width far greater than thickness, equal curvature causes larger strain in width direction than thickness, which may lead to buckling defect[11].
Select infinitesimal element ABCD (Fig. 2) as target object. Let AB and DC be perpendicular to fibers and extend them to intersect at O, with prepreg width as w and the included angle between AB and CD as dα. Let ABCD be tangent plane, and AD and BC as arc. It is concluded that
| $ R = \frac{1}{{{k_g}}} $ | (2) |
| $ AD = \left( {\frac{1}{{{k_g}}} + \frac{w}{2}} \right){\rm{d}}\alpha $ | (3) |
| $ BC = \left( {\frac{1}{{{k_g}}} - \frac{w}{2}} \right){\rm{d}}\alpha $ | (4) |
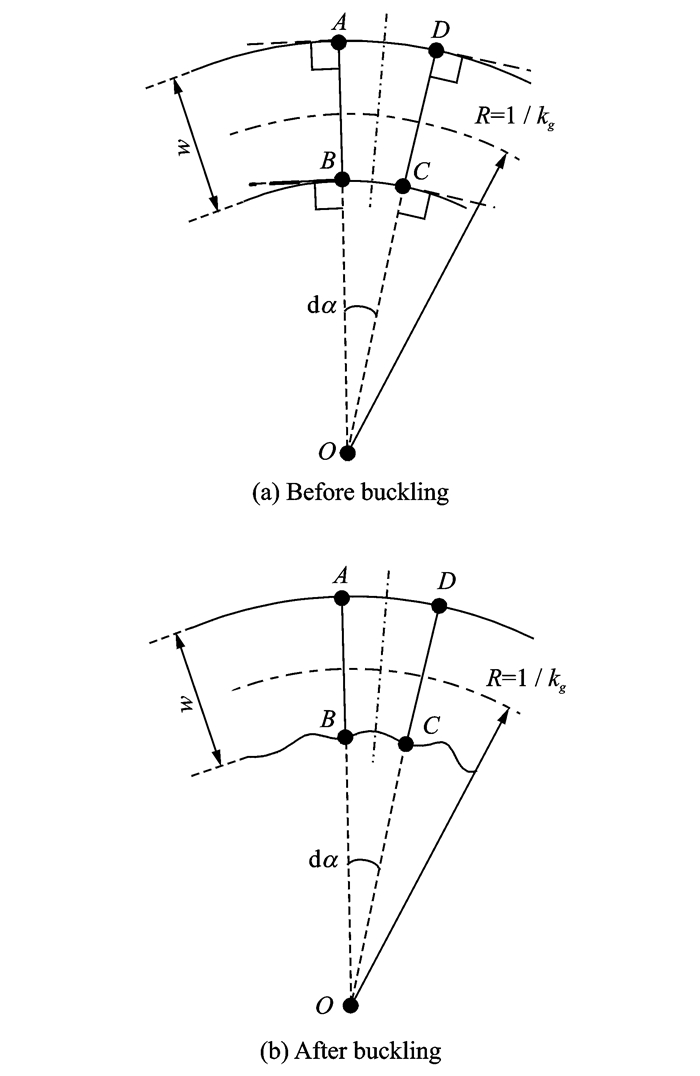
|
Fig. 2 Principle of fiber steering during AFP process |
It is obvious that arc length of AD is larger than that of BC.
Generally speaking, fibers are prone to buckling under compressing stress to release the load. As shown in Fig. 2(b), AD displays tensile strain under tension while BC is under compression. Then BC inclines to buckling and the phenomenon of structure instability may occur. The defect alters the fiber structure and the prepreg no longer maintains the initial mechanical property. Let AD be under no deformation and BC under compressing stress. The compressing strain is illustrated as follows
| $ \varepsilon = \frac{{AD - BC}}{{AD}} = \frac{w}{{\frac{1}{{{k_g}}} + w/2}} $ | (5) |
It is shown that ε is relative to kg and w. Strain ε increases with the increase of kg, and when ε reaches the critical value, buckling takes place. According to fiber buckling model, it is vital to keep AFP path curvature in a relative low standard for the sake of processing quality[12].
1.2 Layup quality analysis of AFP tool pathCurrent path is able to fit variable parts with mild curvature variation, cylinder, for instance. However, it is a remaining problem that the applicability towards complex part is not satisfied, which mainly embodied in the fiber defects. In these situations, path computed in fixed-angle method has a large curvature variation. It increases the chance of fiber defects and damages the part quality.
For instance, as shown in Fig. 3, a typical aircraft S-inlet has special geometric features. Specifically, it consists of a steep convex with large curvature and a corresponding concave. The shape of S-inlet involved in this paper is very complicated. Because one end cross section of S-inlet is circular, but the other one is rectangular. And the curvature along the central axis direction has great variation. Another feature is the transitional peak-like edge that link adjacent surfaces, which is the area of sharp geometric change as well. Different manufacturing defects take place during fixed-angle placement. As shown in Fig. 4, buckling defects normally appear at the area of the edge, simply because of the sharp path curvature standard. On the other hand, fiber bridging occurs in concave area resulting from the tensile force during process.
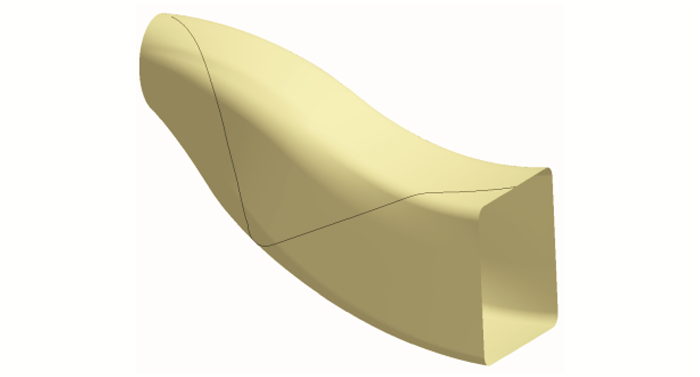
|
Fig. 3 A simplified aircraft S-inlet mould |

|
Fig. 4 Buckling defects in S-inlet AFP manufacturing |
2 Overall Methodology of Global Energy Smoothing Method 2.1 Principles of smoothing
There are two main aspects of curve fairing research: (1) The study of basic fairing principle, which mainly focuses on determining what sort of curve is smooth; (2) fairing algorithms, which are based on a serious of mathematic treatment. During the fairing method, fairing principle determines the mathematic principle as well as the function of algorithms. The general smooth principle is still not certain; however, four common principles are concluded as follows: (1) The curve is C2 continuous; (2) the curve has no redundant inflection points; (3) the curvature changing rate of the curve is even; (4) the curve has small strain energy[13-15].
In general, fairing method have two main method: Global and local fairing method. Energy method, least square method and wavelet method are typical methods of global fairing, of which energy method is widely adopted. The main function of energy method is to decrease the strain energy of target curve under appropriate constrains[15-17]. Curve faired by traditional energy method is tend to approach a straight line if without limit, which has the lowest energy level. The process decreases the global strain energy as well as global curve curvature. Yet the curvature variation changing rate is not considered. The phenomenon of shape curvature transforming exists and it ignores Principle (4). Besides, the tangential including angle between adjacent data points is also relative to curvature. The continuous tangential vector guarantees the smooth orientation transform. And once the included angle is too large, the path may not be smooth and the rotation axis of processing end-effector could rotate sharply, which damage the manufacturing efficiency as well as the fiber orientation.
2.2 Mathematic model of global fairing methodLet a cubic B-spline curve interpolate with the given path data points {Qi0}(i=0, 1, 2, …, n)
| $ {P_0}\left( t \right) = \sum\limits_{j = 0}^{n + 2} {{b_{j0}}{N_{j3}}\left( t \right)} $ | (6) |
where {bj0} is the control vertexes and {t}(t=0, 1, …, n+6) the node vectors. The data parameterization is accomplished by the method of arc length accumulation
| $ {t_0} = {t_1} = {t_2} = {t_3} = 0 $ |
| $ {t_{i + 3}} = \sum\limits_{j = 1}^i {{l_j}} /\sum\limits_{j = 0}^n {{l_j}} \;\;\;\;i = 1,2, \cdots ,n - 1 $ |
| $ {t_{n + 3}} = {t_{n + 4}} = {t_{n + 5}} = {t_{n + 6}} = 1 $ |
where lj=|Qj-1Qj| is the arc length. The target function is defined as
| $ P\left( t \right) = \sum\limits_{j = 0}^{n + 2} {{b_j}{N_{j3}}\left( t \right)} $ | (7) |
The second derivative of Eq.(7) is
| $ P''\left( t \right) = \sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( t \right)} $ | (8) |
where {bj} is the control vertexes of the faired curve.
Regardless of stiffness coefficient, the strain energy E of P(t)(0≪t≪1) is defined as the arc integral of curvature k squared
| $ E = \int {{k^2}{\rm{d}}s} $ | (9) |
Traditional energy method intends to achieve the minimization of Eq.(9) under the limit range. Yet the minimum of E cannot ensure the curvature changing rate is small as well. In order to even the curvature variation, another coefficient D is introduced
| $ \begin{array}{*{20}{c}} {{d_i} = \frac{{{k_{i + 1}} - {k_i}}}{{{l_{i + 1}}}} - \frac{{{k_i} - {k_{i - 1}}}}{{{l_i}}}\;\;\;i = 1,2, \cdots ,n - 1}\\ {D = \sum\limits_{k = 1}^{n - 1} {d_k^2} } \end{array} $ | (10) |
where ki represents the relative curvature at Pi=P(ti+3). It is notable that, when di reaches 0, ki-1, ki and ki+1 vary linearly with the arc length. And the curvature variation around Pi decreases with the value of di. In conclusion, the coefficient D reflects the curvature changing rate of target curve and the new objective function is defined as follows
| $ F = \alpha \int {{k^2}{\rm{d}}s} + \beta \sum\limits_{k = 1}^{n - 1} {d_k^2} + \gamma \sum\limits_{j = 0}^{n + 2} {{{\left( {{b_j} - {b_{j0}}} \right)}^2}} $ | (11) |
where α, β, γ are given constants greater than 0. The smaller of F, the smoother the target curve. Thus, the main task is to achieve the minimum of F under constraint
| $ \begin{array}{l} G = \alpha \int_{{t_0}}^{{t_n}} {{{P''}^2}\left( t \right){\rm{d}}t} + \beta \sum\limits_{i = 1}^{n - 1} {D_i^2} + \gamma \sum\limits_0^{n - 2} {{{\left( {{b_j} - {b_{j0}}} \right)}^2}} + \\ \;\;\;\;\;\;\beta \sum\limits_{k = 1}^{n - 1} {\left\{ {\frac{{\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 4}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 3}}} \right)} } \right]}}{{{l_{k + 1}}}} - } \right.} \\ \;\;\;\;\;\;{\left. {\frac{{\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 3}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{b_j}N{''}_{j3}^2\left( {{t_{k + 2}}} \right)} } \right]}}{{{l_k}}}} \right\}^2} = \\ \;\;\;\;\;\;\alpha \sum\limits_{k = 1}^n {\int_{{t_{k - 1}}}^{{t_k}} {{{\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( t \right)} } \right]}^2}{\rm{d}}t + } } \gamma \sum\limits_{j = 0}^{n + 2} {{{\left( {{b_j} - {b_{j0}}} \right)}^2}} \end{array} $ | (12) |
In Eq.(12), {bi}(i=0, 1, …, n+2) is the only unknown quantity.
To achieve the minimum, set
| $ \begin{array}{l} \frac{{\partial G}}{{\partial {b_i}}} = 2\alpha \sum\limits_{k = 1}^n {\int_{{t_{k - 1}}}^{{t_k}} {{{N''}_{i3}}\left( t \right)\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( t \right)} } \right]{\rm{d}}t} } + 2\gamma \sum\limits_{j = 0}^{n + 2} {\left( {{b_j} - } \right.} \\ \left. {{b_{j0}}} \right) + 2\beta \sum\limits_{k = 1}^{n - 1} {\left\{ {\frac{{\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 4}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 3}}} \right)} } \right]}}{{{l_{k + 1}}}} - } \right.} \\ \left. {\frac{{\left[ {\sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 3}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{b_j}{{N''}_{j3}}\left( {{t_{k + 2}}} \right)} } \right]}}{{{l_k}}}} \right\} \cdot \\ \left\{ {\frac{{\left[ {\sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 4}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 3}}} \right)} } \right]}}{{{l_{k + 1}}}} - } \right.\\ \left. {\frac{{\left[ {\sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 3}}} \right)} - \sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 2}}} \right)} } \right]}}{{{l_k}}}} \right\} = 0 \end{array} $ | (13) |
Set
| $ \begin{array}{l} {\delta _{ik}} = \left\{ {\frac{{\left[ {\sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 4}}} \right)} - \sum\limits_{j = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 3}}} \right)} } \right]}}{{{l_{k + 1}}}} - } \right.\\ \;\;\;\;\;\;\left. {\frac{{\left[ {\sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 3}}} \right)} - \sum\limits_{i = 0}^{n + 2} {{{N''}_{i3}}\left( {{t_{k + 2}}} \right)} } \right]}}{{{l_k}}}} \right\} \end{array} $ |
And Eq.(13) can be simplified as
| $ \begin{array}{l} \frac{{\partial G}}{{\partial {b_i}}} = 2\alpha \sum\limits_{j = 0}^{n + 2} {{b_j}} \sum\limits_{k = 1}^n {\int_{{t_{k - 1}}}^{{t_k}} {{{N''}_{i3}}{{N''}_{j3}}\left( t \right){\rm{d}}t} } + \\ \;\;\;\;\;\;\;\;\;\;2\beta \sum\limits_{j = 0}^{n + 2} {{b_j}} \sum\limits_{k = 1}^{n - 1} {{\delta _{ik}}{\delta _{jk}}} + 2\gamma \sum\limits_{j = 0}^{n + 2} {{{\left( {{b_j} - {b_{j0}}} \right)}^2}} = 0\\ \sum\limits_{j = 0}^{n + 2} {{b_j}} \left[ {2\alpha \sum\limits_{k = 1}^n {\int_{{t_{k - 1}}}^{{t_k}} {{{N''}_{i3}}{{N''}_{j3}}\left( t \right){\rm{d}}t} } + 2\beta \sum\limits_{k = 1}^{n - 1} {{\delta _{ik}}{\delta _{jk}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {2\gamma } \right] = 2\gamma \sum\limits_{j = 0}^{n + 2} {{b_{j0}}} \end{array} $ | (14) |
Eq.(14) is a set of linear equations of {bj}. Set b=(b0, b1, …, bn+2)T and Eq.(14) can be expressed in matrix form
| $ \mathit{\boldsymbol{Ab}} = \mathit{\boldsymbol{c}} $ | (15) |
where A={aij} is the coefficient matrix
| $ \begin{array}{l} {a_{ij}} = 2\alpha \sum\limits_{k = 1}^n {\int_{{t_{k - 1}}}^{{t_k}} {{{N''}_{i3}}{{N''}_{j3}}\left( t \right){\rm{d}}t} } + 2\beta \sum\limits_{k = 1}^{n - 1} {{\delta _{ik}}{\delta _{jk}}} + 2{\gamma _{ij}}\\ \;\;\;\;\;\;\;i,j = 0,1,2, \cdots ,n + 2\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\gamma _{ij}} = \left\{ \begin{array}{l} \gamma \;\;\;\;i = j\\ 0\;\;\;\;i \ne j \end{array} \right. \end{array} $ | (16) |
Vector c=(c0, c1, …, cn+2)T is defined as follows
| $ {c_i} = 2\gamma {b_{i0}}\;\;\;\;\;\;i = 0,1, \cdots ,n + 2 $ |
It is not hard to verify that coefficient matrix A is a symmetric matrix. And once |i-j| > 4, set aij=0, which illustrate that the semi-band width of A is 5. Furthermore, when α and β are far less than γ, A is a symmetric positive definite matrix and it ensure the existence of unique solution to Eq.(15). Above all, the optimized control vertex {bj} can be obtained by solving Eq.(15).
Algorithm procedure
The fairing algorithm process is accomplished by VC ++ 6.0 and Matlab R2014a. The process is composed of the following steps, as shown in Fig. 5.
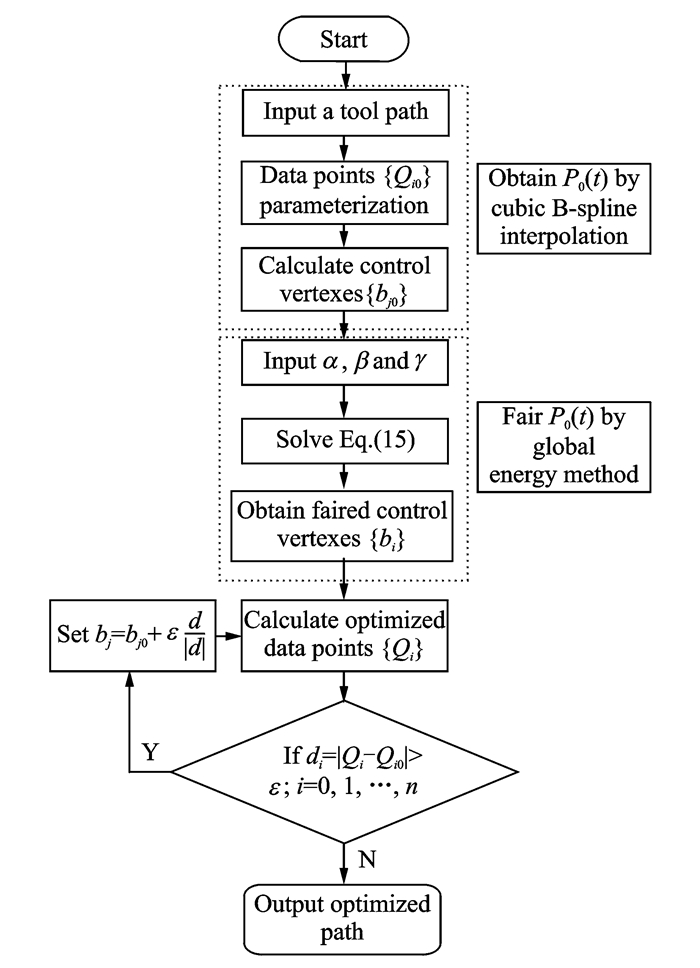
|
Fig. 5 Algorithm steps of global path faring for AFP |
(1) Input the target tool path.
(2) Based on cubic B-spline, interpolate the data points {Qi0}. The whole process mainly includes vector parameterization and the calculation of control vertex {bi0}.
(3) Input the parameter α, β, γ, ε, and compute the faired control vertex {bi} through the global energy method.
(4) Obtain the optimized data points {Qi} and determine the deviation from the original location d=|Qi-Qi0|. Once d is larger than (or less than) ε, set bj=bj0+
(5) Output the optimized path if deviation is under the permitted range.
The fairing function can be shaped by adjusting the parameters. Generally, the value of α should be within a certain range, otherwise the phenomenon of non-convergence will occur during the iteration process. With a smaller β, the curve deviation is smaller but the smooth effect is worse; with a larger β, the smoothness of target curve is better but the deviation is larger.
3 ExperimentThe global energy method is applied to AFP tool path, especially for complex part with sharp curvature variation. The test part is a simplified aircraft S-inlet with a 900 mm width and a 1 660 mm length approximately. The mould is meshed into STL (STereo lithography) and the test path is generated in fixed-angle method. Prepreg used in this experiment is X850 produced by CYTEC, with a tow width of 6.35 mm, and the minimum curvature radius has been proved to be R1 000 mm. Set α=10-7, β=10-7, γ=1 and the maximum deviation ε=1 mm. The detailed analysis is as follows.
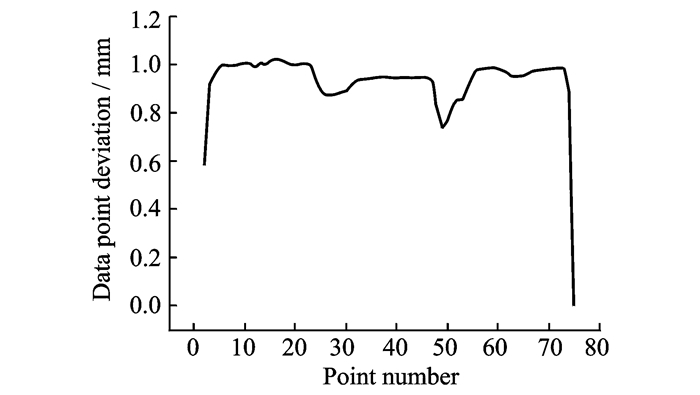
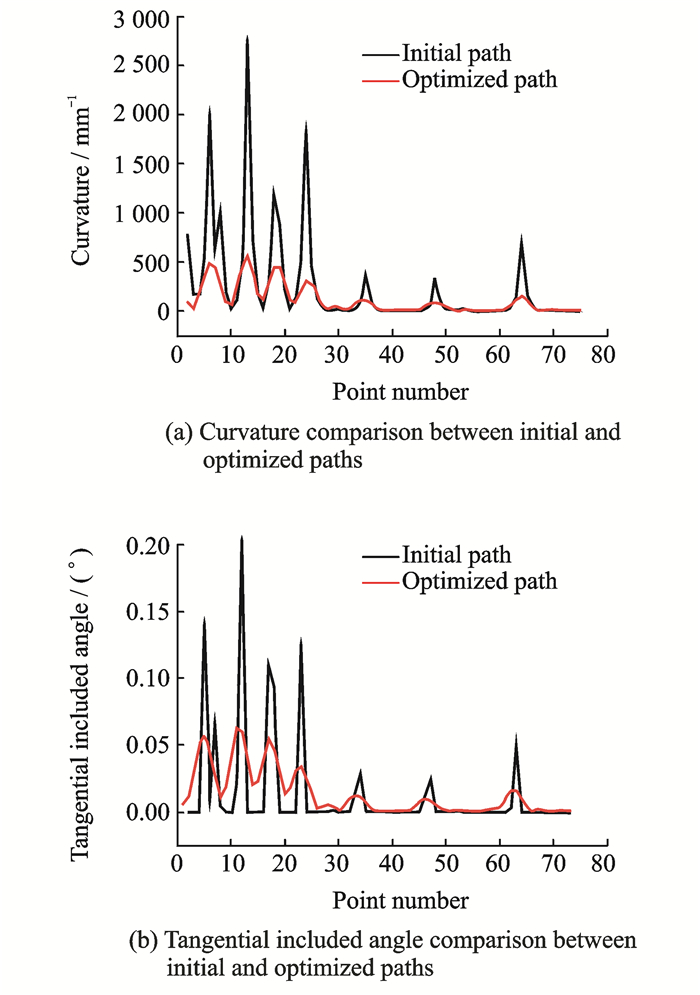
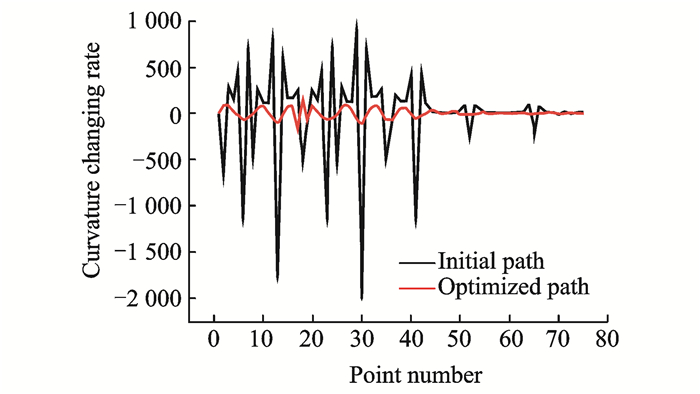
Fig. 6 shows that the deviation is controlled under the given value, which demonstrates the deviation of the optimized path can be regulated precisely. The curvature compairson between the initial and the smoothed curve is presented in Fig. 7(a). It is obvious that the global curve curvature has a sharpe decrease and the change rate is also been controlled. Besides, the tangential included angle between adjacent data points is also been faired, as shown in Fig. 7(b). Both curvature and tangential included angle have a significent decrease especially in peak value. Fig. 8 shows the curvature change rate between initial and faired path, and the result is obvious that the curvature changing range has been decreased.
|
Fig. 6 Deviation of initial path after global faring treatment |
|
Fig. 7 Curvature and tangential included angle comparison between initial and optimized paths |
|
Fig. 8 Curvature change rate comparison between initial and optimized paths |
The practical placement experiment has been carried out with the AFP equipment designed by NUAA. The focus is the area that has large curvature variation which is the peak-like edge and Figs. 9(a) and (b) show the fiber situation at the edge area of initial and faired path, respectively. It is obvious that the fixed-angle path has buckling defect and the deformation degree has been decreased after fairing treatment.

|
Fig. 9 Practical AFP manufacturing comparison |
4 Conclusions
Based on B-spline fairing theory, a global faring method that applied in AFP tool path was presented. Considering the manufacturing process, the algorithm intended to decrease curvature of a complete path and to control the curvature change rate. The main principle of the algorithm was to decrease the global strain energy and to smooth the curvature variation rate. Four parameters α, β, γ and ε were introduced to regulate the fairing function. α, β, γ were relative to the global curve curvature standard, the curvature change rate, the deviation of initial data points, respectively. And ε represented the maximum deviation, which could be adjusted to fit the practical requirement. It was analyzed that the method suceeded in decreasing the path curvature and curvature change rate. Moreover, the tangential angle between adjacent data points was also smoothed, which is relative to fiber steering and manufacturing efficiency. Practical placement experiment had been carried out and the result validated the feasibility of global faring method.
Acknowledgements
This work was supported by the Major Science and Technology Projects of China (No.2016ZX04002-001-07) and Basic Scientific Research Fund (56XAA15057).
| [1] |
GRIMSHAW M N, GRANT C G, DIAZ J M L. Advanced technology tape laying for affordable manufacturing of large composite structures[C]//46th International SAMPE Symposium. Long Beach, CA: SAMPE, 2001: 2484-2494. https://www.researchgate.net/publication/279709442_Advanced_technology_tape_laying_for_affordable_manufacturing_of_large_composite_structures
|
| [2] |
MARSH G. Automating aerospace composites production with fiber placement[J]. Reinforced Plastics, 2011, 55(3): 32-37. DOI:10.1016/S0034-3617(11)70075-3 |
| [3] |
BORGMANN R E, EVANS D. Fiber placement machine: U. S. Patent 7, 353, 853[P]. (2005-05-03)[2008-04-08].
|
| [4] |
SHIRINZADEH B, CASSIDY G, OETOMO D, et al. Trajectory generation for open-contoured structures in robotic fiber placement[J]. Robotics and Computer-Integrated Manufacturing, 2007, 23: 380-394. DOI:10.1016/j.rcim.2006.04.006 |
| [5] |
LEGRAND X, KELLY D, CROSKY A, et al. Optimization of fiber steering in composite laminates using a genetic algorithm[J]. Composite Structures, 2006, 75(1/2/3/4): 524-531. |
| [6] |
CASSIDY G. Robotic fiber placement: Trajectory generation for open contoured structures[D]. Clayton: Monash University, 2003.
|
| [7] |
WEN Liwei, LI Junfei, WANG Xianfeng, et al. Adjustment algorithm based on structural design for automated tape laying and automated fiber placement[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1731-1739. |
| [8] |
FLEISIG R V, SPENCE A D. A constant feed and reduced angular acceleration interpolation algorithm for multi-axis machining[J]. Computer Aided Design, 2001, 33: 1-15. DOI:10.1016/S0010-4485(00)00049-X |
| [9] |
HO M C, HWANG Y R, HU C H. Five-axis tool orientation smoothing using quaternion interpolation algorithm[J]. International Journal of Machine Tools and Manufacture, 2003, 43: 1259-1267. DOI:10.1016/S0890-6955(03)00107-X |
| [10] |
PIECE D, CHANAL H, DUC E. Tool path smoothing of a redundant machine:Application to automated fiber placement[J]. Computer-Aided Design, 2011, 43(2): 122-132. DOI:10.1016/j.cad.2010.09.011 |
| [11] |
BEAKOUA A, CANOA M, LE CAMA J B, et al. Modelling slit tape buckling during automated prepreg manufacturing:A local approach[J]. Composite Structures, 2011, 93(10): 2628-2635. DOI:10.1016/j.compstruct.2011.04.030 |
| [12] |
LOPES C S, GVRDAL Z, CAMANHO P P. Variable-stiffness composite panels:Buckling and first-ply failure improvements over straight-fiber laminates[J]. Computers & Structures, 2008, 86(9): 897-907. |
| [13] |
FARIN G, REIN G, SAPIDIS N, et al. Fairing cubic b-spline curves[J]. Computer-Aided Geometric Design, 1987, 4(1): 91-103. |
| [14] |
SAPIDIS N, FARIN G. Automatic fairing algorithm for b-spline curves[J]. Computer-Aided Design, 1990, 22(2): 121-129. DOI:10.1016/0010-4485(90)90006-X |
| [15] |
POLIAKOFF J F. An improved algorithm for automatic fairing of non-uniform parametric cubic splines[J]. Computer-Aided Design, 1996, 28(1): 59-66. DOI:10.1016/0010-4485(95)00048-8 |
| [16] |
HAGEN H, BONNEAU G P. Variational design of smooth rational bézier curves[J]. Computer-Aided Geometric Design, 1991, 8(5): 393-399. DOI:10.1016/0167-8396(91)90012-Z |
| [17] |
RONG H, CHEN G, ZHANG W. Nonuniform b-spline mesh fairing method[J]. Caddm, 1991(1): 20-28. |
 2018, Vol. 35
2018, Vol. 35


