2. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P. R. China
Most of the products produced today are the accumulated results of several different process stages. With the emphasis on improved quality, Shewhart control charts are widely used for monitoring these process stages. In multistage processes, a Shewhart control chart is often used. If the process stages are independent, this is meaningful. However, in many manufacturing scenarios, the process stages are not independent. The standard Shewhart control charts can not provide the information to determine which process stage or group of process stages has caused the problems (i.e., standard Shewhart control charts could not diagnose dependent manufacturing process stages). Therefore, an alternative approach is to use multivariate control charts such as the Hotelling T2 control chart to monitor all process stages simultaneously. Unfortunately, the process quality characteristics are assumed to be multivariate normal random variables[1]. As pointed out by Asadzadeh[2], this assumption may not hold in some manufacturing scenarios. In addition, although most multivariate quality control charts appear to be effective in detecting out-of-control signals based upon an overall statistic, they can not indicate which stage of the process is out-of-control. In order to overcome these drawbacks, a great deal of research efforts have been devoted to the development of new methods for monitoring dependent process stages. Most notably, an effective and efficient method originally developed by Zhang[3], called cause-selecting control chart, is constructed for values of the outgoing quality Y that is adjusted for the effect of incoming quality X. The advantage of this method is that once an out-of-control signal is given, it is easy to identify the corresponding stage. Therefore, it is more reasonable and beneficial for monitoring multiple dependent processes by taking into consideration the cascade property of multistage process[4-5]. Wade and Woodall[1] discussed that the cause-selecting control chart outperformed the Hotelling T2 chart.
In the implementation of cause-selecting control charts, the most critical issue is how to establish a sound relationship between the incoming and outgoing quality characteristics. However, the relationship between the incoming and outgoing quality characteristics is heavily nonlinear, and it is not easy to directly describe the relationship using a function. Although theoretical derivation or regression analysis may be able to determine the mapping relationship, requirements of adequate understanding of underlying manufacturing processes and strong expertise in mathematical modeling on quality practitioners are far to meet. Moreover, it is even impossible to derivate the relationship between the quality characteristics through the theoretical derivation. Maybe for this reason, all published literature on cause-selecting control charts mainly turn to mathematical regression method, especially the least-squares regression[6-10]. However, this procedure has to use historical data that often contain outliers. Outliers are observations that deviate markedly from others, which arise from heavy-tailed distribution, mixture of distributions, or the errors in collection and recording[5]. Regardlessly, they express the process changes because of the occurrences of assignable causes, or other periods of poor process and workforce performance. The presence of outliers in the data can have a deleterious effect on the method of least squares, resulting in a model that does not adequately fit bulk of the data. Unfortunately, on-site quality practitioners are technical personnel who always are just able to apply it, but not to see why it should not be applied. Hence, these problems have seriously hampered the popularization of cause-selecting control charts in manufacturing industry.
Unlike regression-based models, artificial neural network (ANN) provides an efficient alternative to map complex nonlinear relationships between an input and an output datasets without requiring a detailed knowledge of underlying physical relationships. Little attention has been given to the use of ANNs for identifying the relationship between the incoming and outgoing quality characteristics. This study tries to take the advantage of ANN ensemble (e.g., excellent noise tolerance and strong self-learning capability) to develop an easy-to-deploy, simple-to-implementation and universal model-fitting method for identifying the relationship between the incoming and outgoing quality characteristics. Based on such recognition, a discrete particle swarm optimization-based selective ANN ensemble (PSOSEN) is developed. Utilization of the selective ANN ensemble technique aims to enhance the generalization capability of ANN ensemble in comparison to single ANN learners. Moreover, it can make an overall selective neural network ensemble-based cause-selecting system of control charts easier to be understood and modified, and perform more complex tasks than any of its components (i.e., individual ANNs in the ensemble). Numerical results show that the proposed selective neural network ensemble-based cause-selecting system of control charts may be a promising tool for monitoring dependent process stages without the need for any expertise in theoretical derivation, regression analysis and even ANN as well, which is critical to ordinary quality practitioners to implement cause-selecting control charts.
1 Overview of Cause-Selecting Control Chart 1.1 DefinitionsAt any process stage there are always two kinds of product quality: Overall quality and specific quality[3]. Overall quality is defined as a quality depending on the current subprocess and any previous subprocesses. Specific quality is the one which relies on the current process step. The overall quality consists of two parts: The specific quality and the influence of previous operations on it. The specific quality is a part of the overall quality.
Shewhart control charts are used to discriminate between chance and assignable causes. However, the cause-selecting control chart divides the assignable cause further into the controllable part and the uncontrollable part. Controllable assignable causes are those assignable causes that affect current subprocess but not the previous process stages. The uncontrollable assignable causes are those that affect the previous process stages but cannot be controlled at the current process stage level.
1.2 Basic concepts of cause-selecting control chartIn reviewing the basic principles of cause-selecting control chart, a simple case with two process stages will be used. Let X represent the quality measurement for the first process stage, which follows normal distribution; and Y represents the quality measurement for the second process stage, which follows normal distribution given X. The cause-selecting control chart is then based on values of the outgoing quality Y that have been adjusted for the value of the incoming quality X.
The model relating the two variables X and Y can take many forms. One of the most useful models is the simple linear regression model.
| $ \begin{array}{*{20}{c}} {{Y_i} = {\beta _0} + {\beta _1}{X_i} + {\varepsilon _i}}&{i = 1,2, \cdots ,n} \end{array} $ | (1) |
where β0 and β1 are constants and εi is the normally distributed error with mean zero and variance σ2. In practice, the model parameters β0, β1 and σ are unknown and need to be estimated. The ordinary least squares method is often used for parameter estimation due to its simplicity. In practice, the relationship between X and Y is often unknown and the parameters need to be estimated from an initial sample of n observations.
The cause-selecting control chart is a Shewhart or other type of control chart for the cause-selecting values (donated by Zi) that can be expressed as follows
| $ {Z_i} = {Y_i} - {{\hat Y}_i} $ | (2) |
where
| $ {\rm{CL}} = \bar Z = \frac{1}{n}\sum\limits_{i = 1}^n {{Z_i}} $ | (3) |
The upper and lower control limits for the cause-selecting control chart can then calculated as follows
| $ {\rm{UCL}} = \bar Z + 2.66{{\bar R}_m} $ | (4) |
| $ {\rm{LCL}} = \bar Z - 2.66{{\bar R}_m} $ | (5) |
where
| $ {{\bar R}_m} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {{R_{m,i}}} $ | (6) |
where
| $ {R_{m,i}} = \left| {{Z_{i + 1}} - {Z_i}} \right| $ | (7) |
Once the center line and control limits for the cause-selecting control chart for the current stage have been determined, the chart can be used in conjunction with a Shewhart control chart for the previous stage for two subprocesses. Only according to the diagnosis rules in Table 1, quality practitioners can readily judge their quality responsibility.
| Table 1 Decision rules |
2 Selective Neural Network Ensemble-Enabled Regression Estimation method
In implementing the cause-selecting control chart, the key step is to establish the complex mapping relationship between the preceding stage and the current stage. This section proposes a robust neuro regression estimation method PSOSEN for modeling the relationship between the incoming and outgoing quality characteristics.
ANN ensemble firstly presented by Hansen and Salamon[11] is a learning paradigm where several ANNs are jointly used to solve a same task. The learning paradigm indicates that the generalization performance of an ANN ensemble can be remarkably improved by selecting an optimal subset of individual ANNs in comparison to those of single ANN[12, 13]. In constructing an ANN ensemble, two issues have aroused researchers' concern: How to train component ANNs and how to combine their predictions in some way. In general, the most prevailing methods of training the component ANNs are Bagging and Boosting. The former, presented by Breiman[12] based on bootstrap sampling[14], generates several training sets from the original training set and then trains a component ANN from each of those training sets. The latter, presented by Schapire[15] and further improved by Freund[16] and Freund and Schapire[17], generates a series of component ANNs whose training sets are determined by the performance of former ones.
2.1 Generalization error of neural network ensembleCombining the predictions of component ANNs is meaningful only there is diversity among all component ANNs. It is evident that no further improvement can be obtained when combining ANNs with identical performance. Consequently, in order to pursue the effective ensemble goal, the individual ANNs must be as accurate and diverse as possible[18]. The predication of an ensemble can thus be obtained according to the following expression
| $ \hat y\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^T {{w_i}{y_i}\left( \mathit{\boldsymbol{x}} \right)} $ | (8) |
subjective to
| $ \sum\limits_{i = 1}^T {{w_i}} = 1 $ | (9) |
| $ 0 \le {w_i} \le 1 $ | (10) |
where T is the population size of available candidate networks, yi(x) the actual output of the ith component neural network when the input vector x is given, and wi a weight assigned to the ith component neural network.
The generalization error Ei(x) of the ith individual network on input vector x can be expressed as
| $ {E_i}\left( \mathit{\boldsymbol{x}} \right) = {\left[ {{y_i}\left( \mathit{\boldsymbol{x}} \right) - d\left( \mathit{\boldsymbol{x}} \right)} \right]^2} $ | (11) |
where d(x) is the desired output when the input vector x is given.
The weighted average of the generalization errors E(x) of the individual component ANNs on input vector x can be expressed as
| $ \bar E\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^T {{w_i}{E_i}\left( \mathit{\boldsymbol{x}} \right)} $ | (12) |
The weighted average of the ambiguities of the selected component ANNs on the input x can be expressed as
| $ \bar A\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^T {{w_i}{A_i}\left( \mathit{\boldsymbol{x}} \right)} $ | (13) |
with
| $ {A_i}\left( \mathit{\boldsymbol{x}} \right) = {\left[ {{y_i}\left( \mathit{\boldsymbol{x}} \right) - \hat y\left( \mathit{\boldsymbol{x}} \right)} \right]^2} $ | (14) |
where Ai(x) is the ambiguity of the ith individual network on the input x.
Thus the generalization error for the ensemble can be expressed as
| $ \hat E = \bar E - \bar A $ | (15) |
From examination of the above equation, it can be easily concluded that the increase in the ambiguity will induce decrease in the generalization, it generalization error of individual component network is not increased. This inspires the authors to adopt two strategies to enhance the overall generalization of the ensemble: One is to utilize component ANNs with different architecture, instead of identical numbers of hidden layer nodes; another is to train individual networks on different training data.
2.2 Particle swarm optimization based selective neural network ensembleIn PSOSEN, instead of attempting to design an ensemble of independent networks directly, several accurate and error-independent networks are initially created by using modified Bagging method. Given such some networks, PSOSEN aims to select the subset formed accurate and diverse networks by using discrete PSO algorithm[19]. In PSOSEN, three main steps have been considered: (1) Creation of candidate component ANNs; (2) selection of an optimal subset from a group of promising component ANNs; and (3) combining the predictions of component ANNs in the ensemble.
2.2.1 Creation of component ANNsFor the effective ensemble, the candidate component ANNs in the ensemble must be as accurate and diverse as possible. Therefore, this study uses Bagging method on the training set to generate a group of ANNs. During the training process, the generalization error of each ANN is estimated in each epoch on a testing set. If the error does not change in consecutive five epochs, the training of the ANN is terminated in order to avoid overfitting. Moreover, this study proposes an automatic design scheme, in which each candidate ANN with two hidden-layers is defined over a wide architecture space: The number of neurons in each hidden layer is evolutionarily determined from 5 to 30. These disposals may help escape the tedious process of searching for the optimal ANN architectures by trial and error, while maintaining the diversity of candidate ANNs.
2.2.2 Selection method of PSOSENRecent research conducted by Zhou et al.[20] indicated that it may be better to ensemble some instead of all of the ANNs. When the number of candidate ANNs is small, one can theoretically investigate the generalization capability of every possible subset of individual ANNs and then select the best subset to constitute an ensemble. However, it is very difficult, if not possible, to use exhaustive search to find an optimal subset since the space of possible subsets is very large (2T-1) if T is a big number. In this study, after several individual ANNs being trained, PSOSEN employs discrete particle swarm optimization (PSO) to select an optimum subset of individual ANNs to constitute an ensemble. Each dimension of a particle in the swarm is encoded by binary bit "vt" (t =1, 2, …, T). Thus, PSOSEN can select the component ANNs according to a selection vector v=(v1, v2, …, vT) that can achieve the minimum generalization error (i.e.,
In order to evaluate the performance of the individuals in the evolving population, the generalization error of the ensemble on the validation set is used as the fitness function of PSOSEN.
2.2.3 Combining method of PSOSENAfter a set of component ANNs has been created and selected, an efficient and effective way of combining their predictions should be taken into consideration. The most commonly used combining rules are majority voting, weighted voting, simple averaging, weighted averaging and Bayesian rules. In this study, the component predictions for real-valued ANNs are combined via simple averaging rule. The proposed PSOSEN model is outlined as follows.
Step 1 Specify training set S, validation set V, learner L, trials T, parameters of PSOSEN.
Step 2 While the maximum number of trials has not been reached, do
For t =1 to T
(ⅰ) St =bootstrap sample from S
(ⅱ) Nt=L(St)
End For
Step 3 Generate a population of selection vectors.
Step 4 Utilize discrete PSO to evolve the selection population on the validation set V where the fitness of a selection vector w is measured as f(w)=
Step 5 Obtain the evolved best selection vector w*.
Step 6 Output the final selective ensemble
| $ {N^ * }\left( \mathit{\boldsymbol{x}} \right) = {\rm{Ave}}\sum\limits_{w_t^ * = 1} {{N_t}\left( \mathit{\boldsymbol{x}} \right)} $ |
where T bootstrap samples S1, S2, …, ST are generated from the original training set and a component network Nt is trained from each St, a selective ensemble N* is built from N1, N2, …, NT whose output is the average output of the component networks with real-valued output.
3 Performance Evaluation of PSOSENIn order to demonstrate the generalization capability of the PSOSEN, four benchmark regression problems are first tested and its performance is compared with other commonly used methods.
3.1 Benchmark regression problemsFour benchmark regression problems taken from the literature are used for the performance evaluation. The first regression problem is 2-d Mexican Hat proposed by Weston et al.[21] in investigating the performance of support vector machines. There is one continuous attribute. The dataset is generated according to the following equation
| $ y = \frac{{\sin \left| x \right|}}{{\left| x \right|}} + \varepsilon $ | (16) |
where x follows a uniform distribution between -2π and 2π, and ε represents the noise item that follows a normal distribution with mean 0 and variance 1. In our experiments, the training dataset contains 400 instances, the validation dataset contains 200 instances that are randomly selected from the training dataset, and the testing dataset contains 600 instances.
The second regression problem is SinC proposed by Hansen[22] in comparing several ensemble approaches. There is one continuous attribute. The dataset is generated according to the following equation
| $ y = \frac{{\sin x}}{x} + \varepsilon $ | (17) |
where x follows a uniform distribution between 0 and 2π, and ε represents the noise item that follows a normal distribution with mean 0 and variance 1. In our experiments, the training dataset contains 400 instances, the validation dataset contains 200 instances that are randomly selected from the training dataset, and the testing dataset contains 600 instances.
The third regression problem is Plane proposed by Ridgeway et al.[23] in exploring the performance of boosted naive Bayesian regressors. There are two continuous attributes. The dataset is generated according to the following equation
| $ y = 0.6{x_1} + 0.3{x_2} + \varepsilon $ | (18) |
where xi(i=1, 2) follows a uniform distribution between 0 and 1, and ε represents the noise item that follows a normal distribution with mean 0 and variance 1. In our experiments, the training dataset contains 400 instances, the validation dataset contains 200 instances that are randomly selected fromthe training dataset, and the testing dataset contains 600 instances.
The fourth regression problem is Friedman #1 proposed by Breiman[24] in testing the performance of Bagging. There are five continuous attributes. The dataset is generated according to the following equation
| $ \begin{array}{*{20}{c}} {y = 10\sin \left( {{\rm{ \mathsf{ π} }}{x_1}{x_2}} \right) + 20{{\left( {{x_3} - 0.5} \right)}^2} + }\\ {10{x_4} + 5{x_5} + \varepsilon } \end{array} $ | (19) |
where xi(i=1, 2, …, 5) follows a uniform distribution between 0 and 1, and ε represents the noise item that follows a normal distribution with mean 0 and variance 1. In our experiments, the training dataset contains 400 instances, the validation dataset contains 200 instances that are randomly selected from the training dataset, and the testing dataset contains 600 instances.
It should be noted that the training dataset was employed to train component BPNs of PSOSEN, the validation dataset was employed to select the optimized subset of component BPNs, and testing dataset was employed to evaluate the regression performance of PSOSEN.
3.2 Setup of experimental parameters 3.2.1 StandardizationBefore the training dataset is input into BPNs, the dataset preprocessing (i.e., standardization) must be implemented. Standardization is to make input training data into a constant range through a linear transformation process. The standardization is needed, because BPNs can be trained on a certain range of data. In this study, the normalization is used for preprocessing dataset, which makes the input data to be between 0.1 and 0.9 by using the following equation
| $ {{\mathit{\boldsymbol{\bar x}}}_i} = 0.1 + 0.8\left( {\frac{{{\mathit{\boldsymbol{x}}_i} - \min \left( \mathit{\boldsymbol{x}} \right)}}{{\max \left( \mathit{\boldsymbol{x}} \right) - \min \left( \mathit{\boldsymbol{x}} \right)}}} \right) $ | (20) |
where xi is the input vector, x the vectors in the training dataset, and xi the normalized value corresponding to xi.
3.2.2 Parameter setting of component BPNParameters of component BPN in PSOSEN are summarized as follows.
(1) Input layer: The number of input layer neurons is equal to the number of input attributes of the problem to be addressed.
(2) Output layer: The number of output layer neurons is equal to the number of output attributes of the problem to be addressed.
(3) Hidden layer: The double-hidden-layered BPNs are used. The number of hidden layer neurons is evolutionary obtained from 5 to 30.
(4) Activation function: The hyper tangent (tansig) and sigmoid (purelin) functions are used as activation function for the hidden and the output layers, respectively.
(5) Error function: The mean square error (MSE) is used.
(6) Initial connective weight: The initial connective weights are randomly set between [-0.01, 0.01].
(7) Learning rate and momentum factor: The learning rate and momentum factor are set to be 0.1 and 0.4, respectively. The ratio to increase learning rate and ratio to decrease learning rate are set to be 1.05 and 0.7, respectively.
(8) Training algorithm: The trainlm is adopted here for training of the BPNs.
(9) Learning termination conditions: The training of the BPN is terminated when they reach a pre-determined learning number or if the error does not change in consecutive 10 epochs. In this study, the maximum learning number of BPN is set at 1 000.
(10) Tries of candidate BPNs: In the first step of constructing PSOSEN, the number of candidate BPNs is considered as 20 in this study.
3.2.3 Parameter setting of PSOParameters of discrete PSO are set as follows:
(1) Number of particles in discrete PSO: When discrete PSO algorithm is employed to select an optimum subset of individual ANNs to constitute an ensemble, the number of particles is considered as 40 in this study.
(2) Fitness function of discrete PSO: Fitness function of discrete PSO plays a key role in selecting the optimal subset from candidate BPNs. In this study, the generalization error of PSOSEN is used (i.e., fitness =
(3) Acceleration coefficient: Acceleration coefficients c1 and c2 are set as 1.0 and 0.5, respectively (i.e., c1=1.0, c2=0.5).
(4) Iteration number: Maximum number of iterations is set as 100.
(5) Inertia weight: For the balance between the global exploration and local exploitation of the swarm, the inertia weight w is set to decrease as the generation number increases from 0.8 to 0.2.
(6) Inertia velocity: The inertia velocity v is also set to decrease as the generation number increases during the optimization run from 4 to -4.
3.3 Experimental resultsThe training dataset was used to train component BPNs of PSOSEN.The validation set was used to select the optimized subset of component BPNs. And testing set was used to evaluate the regression performance of PSOSEN. For the purpose of restricting the random effects, the experiments of three approaches were compared on each benchmark problem independently in 20 runs. Comparisons of the proposed PSOSEN with The Best BPN (i.e., the component BPN showing the best training performance among all component BPNs), and Ensemble All (i.e., the average of the outputs of all component BPNs) are presented in Table 2 in terms of the average mean squared error (donated by AMSE) on the testing dataset during the whole 20 independent runs. In order to demonstrate the stability of PSOSEN, the standard deviation of the AMSE (donated by STD) is also provided in Table 2. It is worth noting that each ensemble generated by Ensemble All contains twenty component BPNs. The average number of component BPNs used by PSOSEN in constituting an ensemble is also shown in Table 2. With respect to the AMSE in the training and testing procedure, the results obtained demonstrate that the AMSE of PSOSEN is significantly better than the best BPN and Ensemble All on almost all the regression problems. This indicates that PSOSEN has better generalization performance compared with those of single BPN and the commonly used Ensemble All. Moreover, PSOSEN generated ANN ensembles with far smaller sizes. For these four regression problems, namely 2-d Mexican Hat, SinC, Plane and Friedman #1, the size of the ensembles generated by PSOSEN is about only 38% (7.53/20.0), 30% (6.08/20.0), 41% (8.14/20.0) and 36% (7.13/20.0) of the size of the ensembles generated by Ensemble All. Thus, the second step (i.e., selection of an optimal subset from a group of promising component ANNs) for constructing PSOSEN plays a crucial role in improving the regression performance of PSOSEN. From the given results, the proposed PSOSEN may be a promising tool for the regression problems.
| Table 2 Experiment results of The Best BPN, Ensemble All and DPSOSEN |
4 Case Study
In this section, an example of producing roller workpieces is used to demonstrate how the developed selective neural network ensemble based cause-selecting control charts can play a role in monitoring dependent process stages. The structure and size of the roller part is shown in Fig. 1. The procedure of process planning consists of casting, drilling, inspection, rust proof, and semi-finished products. To simplify the demonstration, this case study focuses on the first two stages of the roller manufacturing process, namely casting and drilling. At the first process stage, machining operation of casting is to produce the rough metal castings. At the second process stage, semi-automatic machines specifically developed for the manufacturing of roller parts are employed to machine both the inner hole and the end face simultaneously from both ends of the roller using the specifically developed combined drills. In addition, the inner diameters were inspected with the help of special gauges. All machining operations were based on the outer cylindrical surface that was placed and clamped on jigs and fixtures to serve as a benchmark location. Apparently, the larger the cylindricity error on a roller surface is, the larger the concentricity error between the outer diameter and inner diameter of the roller becomes, and vice versa. Hence, it can be concluded that the amount of cylindricity error of the roller surface have a statistically significant effect on the occurrences of the concentricity error between the outer diameter and inner diameter of the roller.
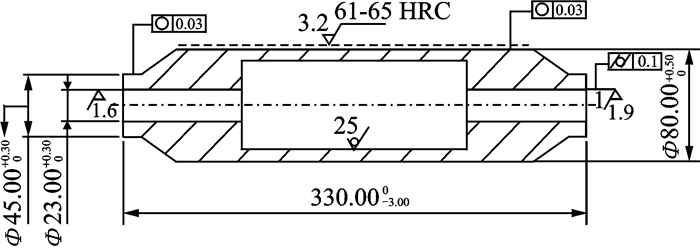
|
Fig. 1 Structure and size of the roller part |
The 48 data points of two quality measurements of interest (i.e., cylindricity and concentricity) are collected and given in Table 3, where X represents the quality measurement of interest (i.e., cylindricity) for the first operation and Y the quality measurement of interest (i.e., concentricity) for the second operation. The first 18 of these data points are used for training dataset and validation dataset of PSOSEN to establish the relationship between the two quality measurements and to calculate the control limits since these points are obtained when the process is in control, and the last 30 of these data points are used as the testing dataset. The relationship between the cylindricity and the concentricity is found using PSOSEN with Y as the dependent quality variable and X as the independent quality variable.
| Table 3 Cylindricity and concentricity of roller workpiece |
Fig. 2 show a comparison between the estimated regression concentricity by PSOSEN and the measured concentricity from the last 30 observations of the experimental dataset. The result indicates that the concentricity estimated by PSO SEN in general agrees with the values of measured concentricity, which further approves the good regression performance of PSOSEN, although there is potential for further improvement in generalization of PSOSEN. The case study has identified two major reasons for the fact that the estimated regression concentricity failed to closely agree with the values of measured concentricity: (1) The residuals between the estimated regression concentricity and the measured concentricity are the cause-selecting values, which partially reflecting the effect of incoming quality measurements on the outgoing quality measurements; (2) less in-control data points are available for training of component BPNs, which to some extent restricts the the generalization capability of component BPNs in PSOSEN.
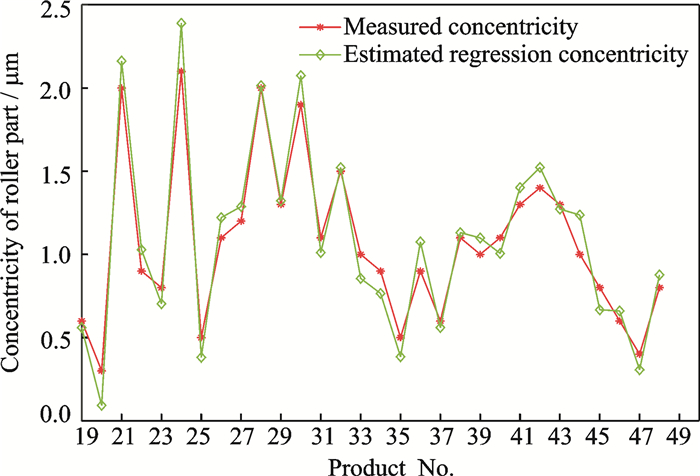
|
Fig. 2 Measured and predicted concentricity for testing dataset |
The next step is to calculate the estimated regression values for the cylindricity and the cause-selecting values Zi for the last 30 observations. The cause-selecting values Zi are given in Table 4.
| Table 4 Cause-selecting values |
| $ \left\{ \begin{array}{l} {\rm{CL}} = \bar Z = 0.009\\ {\rm{UCL}} = \bar Z + 2.66{{\bar R}_m} = 0.448\\ {\rm{LCL}} = \bar Z - 2.66{{\bar R}_m} = - 0.430 \end{array} \right. $ |
By examining the Shewhart control chart for the cylindricity given in Fig. 3, it can be seen that four points, namely points 21, 24, 28 and 32, are out of control. Nevertheless, points 24 and 28 are out of control only on the Shewhart control chart for the cylindricity and they are in control on the cause-selecting control chart. The cause-selecting control chart shown in Fig. 4 detects points 21, and 30 out of control but point 30 in control on the Shewhart control chart for the cylindricity, as shown in Fig. 2. Hence, according to the decision rules in Table 1, one would draw the following conclusions: (1) Point 21 gives signal on all of the control charts, indicating both processes are out of control; (2) points 24, 28 and 32 give signal only on the Shewhart control chart for the cylindricity, indicating the first process is out of control; (3) point 30 gives signal only on the cause-selecting control chart for the concentricity, indicating the second process is out of control.
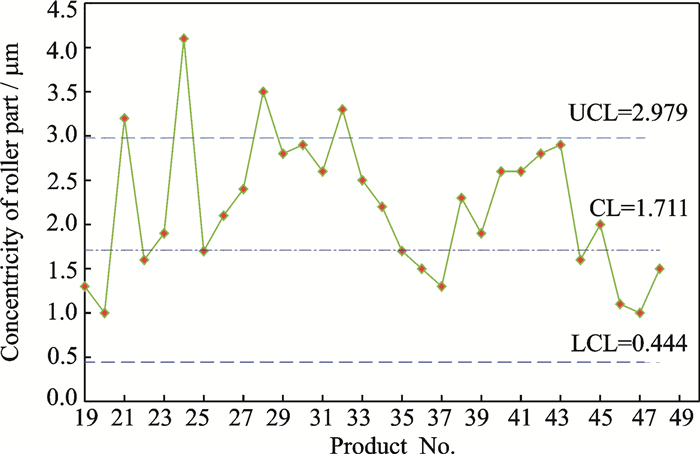
|
Fig. 3 Shewhart control chart for the cylindricity |
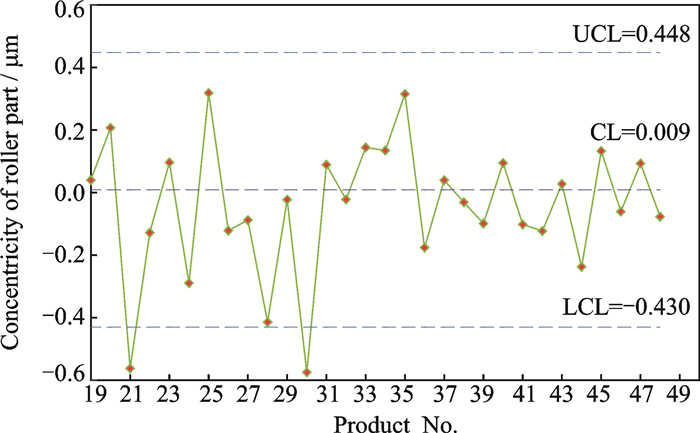
|
Fig. 4 Cause-selecting control chart for the concentricity |
However, the Shewhart control chart for the concentricity is shown in Fig. 5, and the cause-selecting control chart give different conclusions at points 24, 28, and 32. At these points, the Shewhart control chart for the concentricity gives a signal while the cause-selecting control chart does not. This may be explained by the fact that the cause-selecting control chart takes into account the relationship between the two dependent process stages that the Shewhart control chart does not.

|
Fig. 5 Shewhart control chart for the concentricity |
This case study indicates that the cause-selecting system of control charts is an improvement over the use of separate Shewhart control chart for each of dependent process stages, and even ordinary quality practitioners who lack of expertise in theoretical analysis, regression estimation and neural computing can implement it.
5 ConclusionsAvailability of cause-selecting control charts will aid the use of incoming quality measurements and outgoing quality measurements to monitor multiple dependent process stages. A selective neural network ensemble-based cause-selecting system of control charts is developed to distinguish incoming quality problems and problems in the current stage of a manufacturing process. Numeric results show that the proposed scheme is an improvement over the use of separate Shewhart charts for each of dependent process stages, and even ordinary technical personnel who lack of expertise in theoretical analysis, regression estimation and neural computing can implement it. The proposed scheme may be a promising tool for the rapid monitoring of multiple dependent process stages.
The developed selective neural network ensemble-based cause-selecting system of control charts is employed for the case when there is only one single assignable cause. If the quality characteristic at current process stage is the function of multiple assignable causes, this is the cause-selecting system with multiple causes where multiple cause-selecting control charts needs to be implemented. In our future research, it is interesting to extend the proposed scheme to handle the manufacturing processes with multiple assignable causes and multivariate inputs from the previous stage.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (No.51775279), the Fundamental Research Funds for the Central Universities (Nos.1005-YAH15055, NS2017034), the China Postdoctoral Science Foundation (No.2016M591838), the Natural Science Foundation of Jiangsu Province (No.BK20150745), and the Postdoctoral Science Foundation of of Jiangsu Province (No.1501024C). The author would like to acknowledge the helpful comments and suggestions of the reviewers.
| [1] |
WADE M R, WOODALL W H. A review and analysis of cause-selecting control chart[J]. Journal of Quality Technology, 1993, 25(3): 597-602. |
| [2] |
ASADZADEH S, AGHAIE A, SHAHRIARI H. Monitoring dependent process steps using robust cause-selecting control charts[J]. Quality and Reliability Engineering International, 2009, 25: 851-874. DOI:10.1002/qre.v25:7 |
| [3] |
ZHANG G X. A new diagnosis theory with two kinds of quality[J]. Total Quality Management, 1990, 1(2): 249-257. |
| [4] |
HAWKINS D M. Regression adjustment for variables in multivariate quality control[J]. Journal of Quality Technology, 1993, 25(3): 170-182. |
| [5] |
SHU L, TSUNG F. On multistage statistical process control[J]. Journal of the Chinese Institute of Industrial Engineers, 2003, 20(1): 1-8. |
| [6] |
JOANNE M S, ANN M, MARY R L. Measuring performance in multi-stage service operations:An application of cause selecting control charts[J]. Journal of Operations Management, 2006, 24(5): 711-727. DOI:10.1016/j.jom.2005.04.003 |
| [7] |
SHERVIN A, ABDOLLAH A, HAMID S. Monitoring dependent process steps using robust cause-selecting control charts[J]. Qual Reliab Engng Int, 2009, 25: 851-874. DOI:10.1002/qre.v25:7 |
| [8] |
YANG S F, YEH J T. Using cause selecting control charts to monitor dependent process stages with attributes data[J]. Expert Systems with Applications, 2011, 38(1): 667-672. DOI:10.1016/j.eswa.2010.07.018 |
| [9] |
AMIRI A, NIKZAD E. Statistical analysis of total process capability index in two-stage processes with measurement errors[C]//International Conference on Industrial Engineer, 2015, 2(1): 1-6.
|
| [10] |
SOLEYMANI P, AMIRI A. Fuzzy cause selecting control charts for phase Ⅱ monitoring of a two stage process[J]. International Journal of Industrial and Systems Engineering, 2017, 25(3): 404-422. DOI:10.1504/IJISE.2017.10002585 |
| [11] |
HANSEN L K, SALAMON P. Neural network ensembles[J]. IEEE Trans Pattern Analysis and Machine Intelligence, 1990, 12(10): 993-1001. DOI:10.1109/34.58871 |
| [12] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [13] |
KROGH A, VEDELSBY J. Neural network ensembles cross validation, and active learning[C]//Advances in neural information processing systems 7. Denver, CO, Cambridge MA: MIT Press, 1995: 231-238.
|
| [14] |
EFRON B, TIBSHIRANI R. An introduction to the Bootstrap[M]. New York: Chapman & Hall, 1993.
|
| [15] |
SCHAPIRE R E. The strength of weak learnability[J]. Machine Learning, 1990, 5(2): 197-227. |
| [16] |
FREUND Y. Boosting a weak algorithm by majority[J]. Information and Computation, 1995, 121(2): 256-285. DOI:10.1006/inco.1995.1136 |
| [17] |
FREUND Y, SCHAPIRE R E. A decision-theoretic generalization of on-line learning and an application to boosting[J]. Journal of Computer and System Sciences, 1997, 55(1): 119-139. DOI:10.1006/jcss.1997.1504 |
| [18] |
PERRONE M P, COOPER L N. When networks disagree: Ensemble method for neural networks[C]//Artificial Neural Networks for Speech and Vision. New York: Chapman & Hall, 1993: 126-142.
|
| [19] |
KENNEDY J, EBERHART R. A discrete binary version of the particle swarm optimization[C]//Proceedings of the IEEE international conference on computational cybernetics and simulation. Piscataway, NJ: IEEE Press, 1997: 4104-4108.
|
| [20] |
ZHOU Z H, WU J X, TANG W. Ensembling neural networks:Many could be better than all[J]. Artificial Intelligence, 2002, 137(1/2): 239-263. |
| [21] |
WESTON J A E, STITSON M O, GAMMERMAN A, et al. Experiments with support vector machines: CSD-TR-96-19[R]. London: Royal Holloway University of London, 1996.
|
| [22] |
HANSEN J V. Combining predictors: Meta machine: learning methods and bias/variance and ambiguity decompositions[D]. Denmark: University of Aarhus, 2000.
|
| [23] |
RIDGEWAY G, MADIGAN D, RICHARDSON T. Boosting methodology for regression problems[C]//Proceedings of the 7th International Workshop on Artificial Intelligence and Statistics (AISTATS-99). Fort Lauderdale, FL: [s.n.], 1999: 152-161.
|
| [24] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
 2018, Vol. 35
2018, Vol. 35


