Cooperative relaying, as a promising technology to improve spectral efficiency and link reliability, has attracted much attentions [1, 2]. In a cooperative communication system, the relay aids to the transmission of two nodes with different protocols and brings about diversity gain. Amplify-and-forward (AF) is one of the relaying protocols, where the relay amplifies and transfers the signals sent by the source to the destination. For its simple implementation, AF has been widely employed in cooperative communication.
Space shift keying (SSK) activates only one antenna to transmit information at any time slot, so that the need for transmit antenna synchronization and inter-channel interference can be eliminated [3, 4]. In SSK, the active transmit antenna index is the unique way to convey information. Thereby, the optimal detection at the receiver only needs to detect antenna indices. For lack of the symbol detection, the receiver complexity of SSK is decreased [5].
Considering the low complexity of SSK and the diversity gain brought by cooperative relaying, the combination of SSK and cooperative communication has been proposed to further enhance the performance [6-9]. In Ref. [6], the cooperative SSK system with AF and decode-and-forward relaying was presented, and the average bit error rate (BER) expressions are derived. Based on the conventional AF protocol, Refs. [6, 7] proposed an opportunistic AF relaying scheme for the cooperative SSK system, where the best relay is chosen to transmit signals. Spatial modulation (SM) is an extension of SSK that simultaneously exploits antenna indices and constellation symbols to convey information [8]. In Refs. [9, 10], SM is introduced into the cooperative system, and the corresponding BER performance is analyzed. The above works all assume that the channel state information (CSI) is accurately estimated at the receiver, while in particular the influence of channel-estimation error needs to be considered. The performance of cooperative DF and cognitive radio system with SM are studied under the assumption that the imperfect CSI is available at the relay and destination[11, 12]. However, these literatures focus on the SM system with DF and only consider single antenna at the destination for convenient analysis. There are few works addressing the study on the performance of the AF aided SSK (AF-SSK) system, especially in the presence of imperfect channel estimation.
Therefore, in this paper, we will study the performance of the AF-SSK system with multiple receive antennas under imperfect channel estimation, and analyse the effect of channel-estimation error on the performance of AF-SSK system. With the performance analysis, the probability density functions (PDF) and the moment generating functions (MGF) of effective signal-to-noise ratio (SNR), as well as the pairwise error probability (PEP) are derived. Thereby the closed-form expression of average BER is achieved by a union upper bound. Moreover, the asymptotically approximated BER at high SNR is also analyzed. Using this approximation, the diversity gain of this system is further derived for the performance evaluation. Simulation shows that the theoretical BER results can match the simulated values well for different channel-estimation errors, which verifies the correctness of theoretical analysis, and can provide the effective evaluation for the system performance.
1 System ModelThe AF-SSK system combining cooperative AF relaying and SSK is shown as Fig. 1, which consists of a source with Nt transmit antennas, a single-antenna relay and a destination with Nr receive antennas. At the source, the SSK mapper utilizes log2Nt bits to determine the active transmit antenna index i, i∈[1, Nt]. At the destination, with the channel estimate, the optimal detection algorithm based on the maximum likelihood (ML) principle is employed. The output of SSK mapper is given by [13]

|
Fig. 1 Cooperative AF-SSK system model |
| $ {\mathit{\boldsymbol{x}}_i} = {\left[ {\begin{array}{*{20}{c}} 0&0& \cdots &1& \cdots &0 \end{array}} \right]^{\rm{T}}} $ | (1) |
where xi is an Nt-dimensional symbol vector, and the unique nonzero element is in the i-th row, which means that the i-th antenna is activated. Based on the basic idea of cooperative communication, the transmission process is divided into two phases. In the first phase, the source transmits the signal to the relay and the destination. The received signals of the relay and the destination are respectively given by
| $ {y_{{\rm{sr}}}} = \sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{h}}_{{\rm{sr}}}^{\rm{T}}{\mathit{\boldsymbol{x}}_i} + {n_{{\rm{sr}}}} $ | (2) |
| $ {\mathit{\boldsymbol{y}}_{{\rm{sd}}}} = \sqrt {{P_{\rm{s}}}} {\mathit{\boldsymbol{H}}_{{\rm{sd}}}}{\mathit{\boldsymbol{x}}_i} + {\mathit{\boldsymbol{n}}_{{\rm{sd}}}} $ | (3) |
where Ps is the transmission power of the source, hsr a Nt×1 channel vector of source-to-relay link, and Hsd a Nr×Nt channel matrix of source-to-destination link. In the second phase, the relay amplifies the received signal ysr and transfers it to the destination, thus the received signal at the destination is expressed as
| $ {\mathit{\boldsymbol{y}}_{{\rm{rd}}}} = {\mathit{\boldsymbol{h}}_{{\rm{rd}}}}\left( {A{y_{{\rm{sr}}}}} \right) + {\mathit{\boldsymbol{n}}_{{\rm{rd}}}} $ | (4) |
where hrd is a Nr×1 channel vector of relay-to-destination link. The entries of hsr, Hsd and hrd are zero-mean complex Gaussian random variables with variance of δsr2, δsd2 and δrd2, respectively. The variance is defined as δ2=d-α, where d is the distance between two nodes and α is path-loss exponent. nsr, nsd and nrd are zero-mean complex Gaussian noises with the variance of N0. A is the amplification factor and can be written as
In practice, it is hard to achieve the perfect channel information due to the estimation error. For this reason, we will consider imperfect channel estimation in the performance analysis. Let
| $ {h_{mn}} = {{\tilde h}_{mn}} + {e_{mn}} $ | (5) |
where emn is the channel-estimation error, and it follows the complex Gaussian distribution with zero mean and variance σemn2. The estimate
Substituting Eq. (5) into Eqs. (3) and (4), the received signals ysd and yrd can be respectively expressed as
| $ {\mathit{\boldsymbol{y}}_{{\rm{sd}}}} = \sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i + \underbrace {\sqrt {{P_{\rm{s}}}} \mathit{\boldsymbol{e}}_{{\rm{sd}}}^i + {\mathit{\boldsymbol{n}}_{{\rm{sd}}}}}_{{{\mathit{\boldsymbol{\tilde n}}}_{{\rm{sd}}}}} $ | (6) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{y}}_{{\rm{rd}}}} = A\sqrt {{P_{\rm{s}}}} {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^i + }\\ {\underbrace {A\sqrt {{P_{\rm{s}}}} \left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}e_{{\rm{sr}}}^i + {\mathit{\boldsymbol{e}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^i + {\mathit{\boldsymbol{e}}_{{\rm{rd}}}}e_{{\rm{sr}}}^i} \right) + A\left( {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}} + {\mathit{\boldsymbol{e}}_{{\rm{rd}}}}} \right){n_{{\rm{sr}}}} + {\mathit{\boldsymbol{n}}_{{\rm{rd}}}}}_{{{\mathit{\boldsymbol{\tilde n}}}_{{\rm{rd}}}}}} \end{array} $ | (7) |
where
| $ {{\mathit{\boldsymbol{\tilde y}}}_{{\rm{sd}}}} = \sqrt T \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i + {\mathit{\boldsymbol{n}}_1} $ | (8) |
| $ {{\mathit{\boldsymbol{\tilde y}}}_{{\rm{rd}}}} = \sqrt G {{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^i + {\mathit{\boldsymbol{n}}_2} $ | (9) |
where
With the received signals and the channel estimates at the destination, the detection algorithm based on the ML principle is written as [13]
| $ \begin{array}{*{20}{c}} {\hat i = \mathop {\arg \min }\limits_{j \in \left[ {1,{N_{\rm{t}}}} \right]} \left[ {T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^{\rm{2}} - 2\sqrt T {\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{\tilde y}}_{{\rm{sd}}}^{\rm{H}}\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\} + } \right.}\\ {\left. {G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^j} \right|}^2} - 2\sqrt G {\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{\tilde y}}_{{\rm{rd}}}^{\rm{H}}{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^j} \right\}} \right]} \end{array} $ | (10) |
Therefore, the estimate of active transmit antenna index
In this section, the performance of cooperative AF-SSK system in the presence of imperfect channel information will be analyzed, and the closed-form expression of average BER will be derived. Using the detection algorithm in Eq.(10), the antenna index is detected by minimizing Dj, which is expressed as
| $ \begin{array}{*{20}{c}} {{D_j} = T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^{\rm{2}} - 2\sqrt T {\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{\tilde y}}_{{\rm{sd}}}^{\rm{H}}\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\} + }\\ {G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^j} \right|}^2} - 2\sqrt G {\mathop{\rm Re}\nolimits} \left\{ {\mathit{\boldsymbol{\tilde y}}_{{\rm{rd}}}^{\rm{H}}{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^j} \right\}} \end{array} $ | (11) |
If the i-th antenna is activated at the source and the estimate of antenna index at the destination is j, j≠i, then we can obtain
| $ \begin{array}{*{20}{c}} {{D_{j \ne i}} = T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^{\rm{2}} - 2\sqrt {{P_{\rm{s}}}} {\mathop{\rm Re}\nolimits} \left\{ {\sqrt T {{\left( {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i} \right)}^{\rm{H}}}\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j + \mathit{\boldsymbol{n}}_1^{\rm{H}}\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\} + }\\ {G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^j} \right|}^2} - 2\sqrt G {\mathop{\rm Re}\nolimits} \left\{ {\sqrt G {{\left( {\tilde h_{{\rm{sr}}}^i} \right)}^{\rm{H}}}\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2\tilde h_{{\rm{sr}}}^j + } \right.}\\ {\left. {\mathit{\boldsymbol{n}}_2^{\rm{H}}{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^j} \right\}} \end{array} $ | (12) |
If the detection is correct (i.e, j=i), then Eq. (12) can be simplified as
| $ \begin{array}{*{20}{c}} {{D_{j = i}} = T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i} \right\|_{\rm{F}}^{\rm{2}} - 2\sqrt {{P_{\rm{s}}}} {\mathop{\rm Re}\nolimits} \left\{ {\sqrt T \left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i} \right\|_{\rm{F}}^2 + \mathit{\boldsymbol{n}}_1^{\rm{H}}\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i} \right\} + }\\ {G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i} \right|}^2} - 2\sqrt G {\mathop{\rm Re}\nolimits} \left\{ {\sqrt G \left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i} \right|}^2} + } \right.}\\ {\left. {\mathit{\boldsymbol{n}}_2^{\rm{H}}{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}\tilde h_{{\rm{sr}}}^i} \right\}} \end{array} $ | (13) |
With Eqs. (12) and (13), the conditional PEP given by
| $ \begin{array}{*{20}{c}} {{\rm{pep}}\left( {i \to j\left| {{{\mathit{\boldsymbol{\tilde H}}}_{{\rm{sd}}}}} \right.,{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{sr}}}},{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right) = \Pr \left( {{D_{j \ne i}} < {D_{j = i}}} \right) = }\\ {\Pr \left( {T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2 + G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2} < \tilde n} \right)} \end{array} $ | (14) |
where
| $ \begin{array}{*{20}{c}} {\sigma _{\tilde n}^2 = 2\left( {T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j{x_m} - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i{x_q}} \right\|_{\rm{F}}^2 + } \right.}\\ {\left. {G\left\| {{\mathit{\boldsymbol{h}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^j{x_m} - \tilde h_{{\rm{sr}}}^i{x_q}} \right|}^2}} \right)} \end{array} $ | (15) |
Utilizing the PDF of
| $ \begin{array}{*{20}{c}} {{\rm{pep}}\left( {i \to j\left| {{{\mathit{\boldsymbol{\tilde H}}}_{{\rm{sd}}}}} \right.,{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{sr}}}},{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right) =\\ \int_{T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2 + G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2}}^\infty {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}\sigma _{\tilde n}^2} }}\exp \left( { - \frac{{{t^2}}}{{2\sigma _{\tilde n}^2}}} \right){\rm{d}}t} = }\\ {Q\left( {\frac{{T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2 + G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2}}}{{{\sigma _{\tilde n}}}}} \right) = }\\ {Q\left( {\sqrt {\frac{{T\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2 + G\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2}}}{2}} } \right) = }\\ {Q\left( {\sqrt {\frac{{{P_{\rm{s}}}\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2}}{{2\left( {{P_{\rm{s}}}\sigma _{{e_{{\rm{sd}}}}}^2 + {N_0}} \right)}} + \frac{{{P_{\rm{s}}}{P_{\rm{r}}}\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2\frac{{{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2}}}{2}}}{{{P_{\rm{r}}}\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2\left( {{P_{\rm{s}}}\sigma _{{e_{{\rm{sr}}}}}^2 + {N_0}} \right) + \left( {{P_{\rm{r}}}\sigma _{{e_{{\rm{rd}}}}}^2 + {N_0}} \right)\left( {{P_{\rm{s}}}\delta _{{\rm{sr}}}^2 + {N_0}} \right)}}} } \right) = }\\ {Q\left( {\sqrt {\frac{{{P_{\rm{s}}}\left\| {\mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^i - \mathit{\boldsymbol{\tilde h}}_{{\rm{sd}}}^j} \right\|_{\rm{F}}^2}}{{2\left( {{P_{\rm{s}}}\sigma _{{e_{{\rm{sd}}}}}^2 + {N_0}} \right)}} + \frac{{\frac{{{P_{\rm{r}}}\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2}}{{{P_{\rm{r}}}\sigma _{{e_{{\rm{rd}}}}}^2 + {N_0}}}\frac{{{P_{\rm{s}}}{{\left| {\tilde h_{{\rm{sr}}}^i - \tilde h_{{\rm{sr}}}^j} \right|}^2}}}{{2\left( {{P_{\rm{s}}}\sigma _{{\rm{sr}}}^2 + {N_0}} \right)}}}}{{\left( {\frac{{{P_{\rm{r}}}\left\| {{{\mathit{\boldsymbol{\tilde h}}}_{{\rm{rd}}}}} \right\|_{\rm{F}}^2}}{{{P_{\rm{r}}}\sigma _{{e_{{\rm{rd}}}}}^2 + {N_0}}} + C} \right)}}} } \right)} \end{array} $ | (16) |
where
Using
| $ \begin{array}{*{20}{c}} {{\rm{pep}}\left( {i \to j\left| {{\gamma _{{\rm{sd}}}}} \right.,{\gamma _{{\rm{srd}}}}} \right) = Q\left( {\sqrt {{\gamma _{{\rm{sd}}}} + \frac{{{\gamma _{{\rm{sr}}}}{\gamma _{{\rm{rd}}}}}}{{{\gamma _{{\rm{rd}}}} + C}}} } \right) = }\\ {Q\sqrt {{\gamma _{{\rm{sd}}}} + {\gamma _{{\rm{srd}}}}} } \end{array} $ | (17) |
where
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) = \int_0^\infty {\int_0^\infty {{\rm{pep}}\left( {i \to j\left| {{\gamma _{{\rm{sd}}}}} \right.,{\gamma _{{\rm{srd}}}}} \right) \times } } }\\ {{f_{{\gamma _{{\rm{sd}}}}}}\left( \gamma \right){f_{{\gamma _{{\rm{srd}}}}}}\left( \gamma \right){\rm{d}}{\gamma _{{\rm{srd}}}}{\rm{d}}{\gamma _{{\rm{sd}}}} = }\\ {\int_0^\infty {\int_0^\infty {Q\left( {\sqrt { {{\gamma _{{\rm{sd}}}}} ,{\gamma _{{\rm{srd}}}}} } \right){f_{{\gamma _{{\rm{sd}}}}}}\left( \gamma \right){f_{{\gamma _{{\rm{srd}}}}}}\left( \gamma \right){\rm{d}}{\gamma _{{\rm{srd}}}}{\rm{d}}{\gamma _{{\rm{sd}}}}} } } \end{array} $ | (18) |
Based on
| $ {\rm{PEP}}\left( {i \to j} \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^{\frac{{\rm{ \mathsf{ π} }}}{2}} {{M_{{\gamma _{{\rm{sd}}}}}}\left( {\frac{1}{{2{{\sin }^2}\theta }}} \right){M_{{\gamma _{{\rm{srd}}}}}}\left( {\frac{1}{{2{{\sin }^2}\theta }}} \right){\rm{d}}\theta } $ | (19) |
where Mγsd(·) and Mγsrd(·) are MGFs of γsd and γsrd, respectively.
Let t=sinθ and using the transformation of variables, Eq. (19) can be rewritten as
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) = \frac{1}{{{\rm{2 \mathsf{ π} }}}}\int_0^1 {{M_{{\gamma _{{\rm{sd}}}}}}\left( {\frac{1}{{2{t^2}}}} \right){M_{{\gamma _{{\rm{srd}}}}}}\left( {\frac{1}{{2{t^2}}}} \right)\frac{1}{{\sqrt {1 - {t^2}} }}{\rm{d}}t} \cong }\\ {\frac{{N_{\rm{p}}^{ - 1}}}{2}\sum\limits_{u = 1}^{{N_{\rm{p}}}} {{M_{{\gamma _{{\rm{sd}}}}}}\left( {1/2\varphi _u^2} \right){M_{{\gamma _{{\rm{srd}}}}}}\left( {1/2\varphi _u^2} \right)} } \end{array} $ | (20) |
where φu=cos((2u-1)π/(2Np)), and Np is the order of the Chebyshev polynomial [16].
Based on the definitions in Eq. (17), the PDFs of γsd, γsr and γrd over Rayleigh channel are respectively given by
| $ {f_{{\gamma _{{\rm{sd}}}}}}\left( \gamma \right) = \frac{1}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right){{\bar \gamma }_{{\rm{sd}}}}}}{\left( {\frac{\gamma }{{{{\bar \gamma }_{{\rm{sd}}}}}}} \right)^{{N_{\rm{r}}} - 1}}\exp \left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{sd}}}}}}} \right) $ | (21) |
| $ {f_{{\gamma _{{\rm{rd}}}}}}\left( \gamma \right) = \frac{1}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right){{\bar \gamma }_{{\rm{rd}}}}}}{\left( {\frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)^{{N_{\rm{r}}} - 1}}\exp \left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right) $ | (22) |
| $ {f_{{\gamma _{{\rm{sr}}}}}}\left( \gamma \right) = \exp \left( { - \gamma /{{\bar \gamma }_{{\rm{sr}}}}} \right)/{{\bar \gamma }_{{\rm{sr}}}} $ | (23) |
Correspondingly, the cumulative distribution function (CDF) of γsr is obtained by
| $ {F_{{\gamma _{{\rm{sr}}}}}}\left( \gamma \right) = 1 - \exp \left( { - \gamma /{{\bar \gamma }_{{\rm{sr}}}}} \right) $ | (24) |
where
With the PDF of γsd, the corresponding MGF can be derived as
| $ {M_{{\gamma _{{\rm{sd}}}}}}\left( s \right) = \mathscr{L}\left\{ {{f_{{\gamma _{{\rm{sd}}}}}}\left( \gamma \right)} \right\} = {\left( {1 + {{\bar \gamma }_{{\rm{sd}}}}s} \right)^{ - {N_{\rm{r}}}}} $ | (25) |
Using Eqs. (22) and (24), the CDF of γsrd is given by
| $ \begin{array}{*{20}{c}} {{F_{{\gamma _{{\rm{srd}}}}}}\left( \gamma \right) = \Pr \left( {\frac{{{\gamma _{{\rm{sr}}}} + {\gamma _{{\rm{rd}}}}}}{{{\gamma _{{\rm{rd}}}} + C}} < \gamma } \right) = }\\ {\int_0^\infty {{F_{{\gamma _{{\rm{sr}}}}}}\left( {\frac{{\gamma \left( {{\gamma _{{\rm{rd}}}} + C} \right)}}{{{\gamma _{{\rm{rd}}}}}}} \right){f_{{\gamma _{{\rm{rd}}}}}}\left( {{\gamma _{{\rm{rd}}}}} \right){\rm{d}}{\gamma _{{\rm{rd}}}}} = }\\ {1 - \frac{2}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}{{\rm{e}}^{ - \frac{\gamma }{{{{\bar \gamma }_{{\rm{sr}}}}}}}}{{\left( {\sqrt {\frac{{\gamma C}}{{{{\bar \gamma }_{{\rm{sr}}}}{{\bar \gamma }_{{\rm{rd}}}}}}} } \right)}^{{N_{\rm{r}}}}}{K_{{N_{\rm{r}}}}}\left( {2\sqrt {\frac{{\gamma C}}{{{{\bar \gamma }_{{\rm{sr}}}}{{\bar \gamma }_{{\rm{rd}}}}}}} } \right)} \end{array} $ | (26) |
where Kv(·) is the v-th order modified Bessel function of the second kind [17]. Then the MGF of γsrd is derived as
| $ \begin{array}{*{20}{c}} {{M_{{\gamma _{{\rm{srd}}}}}}\left( s \right) = s\mathscr{L}\left\{ {{F_{{\gamma _{{\rm{srd}}}}}}\left( \gamma \right)} \right\} = }\\ {1 - \frac{{s{{\bar \gamma }_{{\rm{sr}}}}{{\bar \gamma }_{{\rm{rd}}}}{N_{\rm{r}}}}}{C}{z^{\left( {{N_{\rm{r}}} + 1} \right)/2}}{{\rm{e}}^{z/2}}{W_{ - \left( {{N_{\rm{r}}} + 1} \right)/2,{N_{\rm{r}}}/2}}\left( z \right)} \end{array} $ | (27) |
where
Substituting Eqs. (25) and (27) into Eq. (20), the average PEP can be written as
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) \cong \frac{{N_{\rm{p}}^{ - 1}}}{2}\sum\limits_{u = 1}^{{N_{\rm{p}}}} {{{\left( {1 + \frac{{{{\bar \gamma }_{{\rm{sd}}}}}}{{2\varphi _u^2}}} \right)}^{ - {N_{\rm{r}}}}}} \times }\\ {\left[ {1 - \frac{{{{\bar \gamma }_{{\rm{sr}}}}{{\bar \gamma }_{{\rm{rd}}}}{N_{\rm{r}}}}}{{2\varphi _u^2C}}{{\hat z}^{\left( {{N_{\rm{r}}} + 1} \right)/2}}{{\rm{e}}^{\hat z/2}}{W_{ - \left( {{N_{\rm{r}}} + 1} \right)/2,{N_{\rm{r}}}/2}}\left( {\hat z} \right)} \right]} \end{array} $ | (28) |
where
| $ \begin{array}{*{20}{c}} {{P_{\rm{e}}} \le \sum\limits_{j = 1}^{{N_{\rm{t}}}} {\sum\limits_{i = 1}^{{N_{\rm{t}}}} {\frac{{N\left( {i \to j} \right)}}{{{N_{\rm{t}}}{{\log }_2}\left( {{N_{\rm{t}}}} \right)}}{\rm{PEP}}\left( {i \to j} \right)} } = }\\ {\left( {{N_{\rm{t}}}/2} \right)PEP\left( {i \to j} \right)} \end{array} $ | (29) |
where N(i→j) is the number of error bits between the actual active antenna index i and the estimate j, and
Substituting Eq. (28) into Eq. (29), the closed-form BER expression of the AF-SSK system with channel estimation error can be derived as
| $ \begin{array}{*{20}{c}} {{P_{\rm{e}}} \le \frac{{{N_{\rm{t}}}}}{{4{N_{\rm{p}}}}}\sum\limits_{u = 1}^{{N_{\rm{p}}}} {{{\left( {1 + \frac{{{{\bar \gamma }_{{\rm{sd}}}}}}{{2\varphi _u^2}}} \right)}^{ - {N_{\rm{r}}}}}} \cdot }\\ {\left[ {1 - \frac{{{{\bar \gamma }_{{\rm{sr}}}}{{\bar \gamma }_{{\rm{rd}}}}{N_{\rm{r}}}}}{{2\varphi _u^2C}}{{\hat z}^{\frac{{{N_{\rm{r}}} + 1}}{2}}}{{\rm{e}}^{\frac{{\hat z}}{2}}}{W_{ - \left( {{N_{\rm{r}}} + 1} \right)/2,{N_{\rm{r}}}/2}}\left( {\hat z} \right)} \right]} \end{array} $ | (30) |
Based on Eq. (30), the theoretical average BER can be achieved, and it is shown to have a good agreement with the corresponding simulation for both imperfect CSI and perfect CSI (i.e., σ2esd=σ2esr=σ2erd=0).
3 Asymptotic BER Analysis and Diversity GainIn this section, the asymptotic performance of the AF-SSK system under large SNR is analyzed, and asymptotically approximated expression of average BER is derived. With this approximation, the diversity gain of the system is attained.
Using the series representation of Kv(·)(which is Eq.(8.446) in Ref.[17]), Kv(2x) with small x can be approximated as
| $ \begin{array}{*{20}{c}} {{K_v}\left( {2x} \right) \approx \frac{1}{2}\sum\limits_{j = 0}^{v - 1} {{{\left( { - 1} \right)}^j}\frac{{\left( {v - j - 1} \right)!}}{{j!}}{x^{2k - v}}} + }\\ {{{\left( { - 1} \right)}^{v + 1}}\frac{{{x^v}}}{{v!}}\left[ {\ln \left( x \right) - \frac{1}{2}\psi \left( 1 \right) - \frac{1}{2}\psi \left( {v + 1} \right)} \right]} \end{array} $ | (31) |
where ψ(·)is the psi function[17].
Plugging Eq. (31) into Eq. (26), and considering
| $ \begin{array}{*{20}{c}} {{F_{{\gamma _{{\rm{srd}}}}}}\left( \gamma \right) \approx 1 - \frac{{{{\rm{e}}^{ - \frac{\gamma }{{{\gamma _{{\rm{sr}}}}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}\left[ {\sum\limits_{k = 0}^{{N_{\rm{r}}} - 1} {\frac{{\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right)}}{{\mathit{\Gamma }\left( {k + 1} \right)}}{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^k}} - } \right.}\\ {\left. {\frac{{{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^{{N_{\rm{r}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}} + 1} \right)}}\left( {\ln \left( {\frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right) - \psi \left( 1 \right) - \psi \left( {{N_{\rm{r}}} + 1} \right)} \right)} \right] \approx }\\ {1 - {{\rm{e}}^{ - \frac{\gamma }{{{\gamma _{{\rm{sr}}}}}}}} - \frac{{{{\rm{e}}^{ - \frac{\gamma }{{{\gamma _{{\rm{sr}}}}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}\left[ {\sum\limits_{k = 0}^{{N_{\rm{r}}} - 1} {\frac{{\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right)}}{{\mathit{\Gamma }\left( {k + 1} \right)}}{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^k}} - } \right.}\\ {\left. {\frac{{{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^{{N_{\rm{r}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}} + 1} \right)}}\left( {\ln \left( {\frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right) - \psi \left( 1 \right) - \psi \left( {{N_{\rm{r}}} + 1} \right)} \right)} \right] \approx }\\ {\frac{\gamma }{{{{\bar \gamma} _{{\rm{sr}}}}}} - \frac{1}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}\left[ {\sum\limits_{k = 0}^{{N_{\rm{r}}} - 1} {\frac{{\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right)}}{{\mathit{\Gamma }\left( {k + 1} \right)}}{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^k}} - } \right.}\\ {\left. {\frac{{{{\left( { - \frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^{{N_{\rm{r}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}} + 1} \right)}}\left( {\ln \left( {\frac{\gamma }{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right) - \psi \left( 1 \right) - \psi \left( {{N_{\rm{r}}} + 1} \right)} \right)} \right]} \end{array} $ | (32) |
where the third approximate equation is obtained based on the approximation that
With the Laplace transform, the MGF of γsrd is approximated as
| $ \begin{array}{*{20}{c}} {{M_{{\gamma _{{\rm{srd}}}}}}\left( s \right) \approx \frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}s}} - \frac{1}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}\left[ {\sum\limits_{k = 1}^{{N_{\rm{r}}} - 1} {\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right){{\left( { - s{{\bar \gamma }_{{\rm{rd}}}}} \right)}^{ - k}}} + } \right.}\\ {\left. {{{\left( { - s{{\bar \gamma }_{{\rm{rd}}}}} \right)}^{ - {N_{\rm{r}}}}}\left( {\ln \left( {s{{\bar \gamma }_{{\rm{rd}}}}} \right) + \psi \left( 1 \right)} \right)} \right]} \end{array} $ | (33) |
Substituting Eq.(33) and the approximation
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) \approx \frac{{{2^{{N_{\rm{r}}}}}}}{{{\rm{ \mathsf{ π} }}{{\bar \gamma }_{{\rm{sd}}}}^{{N_{\rm{r}}}}}}\int_0^{{\rm{ \mathsf{ π} }}/2} {\left[ {\frac{2}{{{{\bar \gamma }_{{\rm{sr}}}}}}{{\left( {\sin \theta } \right)}^{2{N_{\rm{r}}} + 2}} - } \right.} }\\ {\sum\limits_{k = 1}^{{N_{\rm{r}}} - 1} {\frac{{\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right){{\left( { - 2} \right)}^k}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)\bar \gamma _{{\rm{rd}}}^k}}{{\left( {\sin \theta } \right)}^{2{N_{\rm{r}}} + 2k}}} - {{\left( { - \frac{4}{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^{{N_{\rm{r}}}}} \times }\\ {\left. {\frac{{{{\left( {\sin \theta } \right)}^{4{N_{\rm{r}}}}}}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)}}\left( {\psi \left( 1 \right) + \ln \left( {\frac{{{{\bar \gamma }_{{\rm{rd}}}}}}{2}} \right) - 2\ln \sin \theta } \right)} \right]{\rm{d}}\theta } \end{array} $ | (34) |
With (3.621.3) and (4.387.4) in Ref.[17], we can obtain
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) \approx {{\left( {\frac{2}{{{{\bar \gamma }_{{\rm{sd}}}}}}} \right)}^{{N_{\rm{r}}}}}\left[ {\frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}}}\frac{{\left( {2{N_{\rm{r}}} + 1} \right)!!}}{{\left( {2{N_{\rm{r}}} + 2} \right)!!}} + } \right.}\\ {\sum\limits_{k = 1}^{{N_{\rm{r}}} - 1} {\frac{{{{\left( { - 2} \right)}^{k - 1}}\mathit{\Gamma }\left( {{N_{\rm{r}}} - k} \right)}}{{\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right){{\left( {{{\bar \gamma }_{{\rm{rd}}}}} \right)}^k}}}\frac{{\left( {2{N_{\rm{r}}} + 2k - 1} \right)!!}}{{\left( {2{N_{\rm{r}}} + 2k} \right)!!}}} - }\\ {{{\left( { - \frac{2}{{{{\bar \gamma }_{{\rm{rd}}}}}}} \right)}^{{N_{\rm{r}}}}}\frac{{\left( {4{N_{\rm{r}}} - 1} \right)!!}}{{2\mathit{\Gamma }\left( {{N_{\rm{r}}}} \right)\left( {4{N_{\rm{r}}}} \right)!!}}\left( {\ln \left( {2{{\bar \gamma }_{{\rm{rd}}}}} \right) + } \right.}\\ {\left. {\left. {\psi \left( 1 \right) + 2\sum\limits_{l = 1}^{4{N_{\rm{r}}}} {\frac{{{{\left( { - 1} \right)}^l}}}{l}} } \right)} \right]} \end{array} $ | (35) |
For Nr=1, the average PEP expression of Eq.(35) under high SNR can be rewritten as
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) \approx }\\ {\frac{3}{{4{{\bar \gamma }_{{\rm{sd}}}}}}\left[ {\frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}}} + \frac{1}{{{{\bar \gamma }_{{\rm{rd}}}}}}\left( {\ln \left( {2{{\bar \gamma }_{{\rm{rd}}}}} \right) + \psi \left( 1 \right) - \frac{7}{6}} \right)} \right]} \end{array} $ | (36) |
Thus the approximate average BER is obtained by
| $ {P_{\rm{e}}} \approx \frac{{3{N_t}}}{{8{{\bar \gamma }_{{\rm{sd}}}}}}\left[ {\frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}}} + \frac{1}{{{{\bar \gamma }_{{\rm{rd}}}}}}\left( {\ln \left( {2{{\bar \gamma }_{{\rm{rd}}}}} \right) + \psi \left( 1 \right) - \frac{7}{6}} \right)} \right] $ | (37) |
For Nr≥2, the average PEP can be further simplified as
| $ \begin{array}{*{20}{c}} {{\rm{PEP}}\left( {i \to j} \right) \approx }\\ {{{\left( {\frac{2}{{{{\bar \gamma }_{{\rm{sd}}}}}}} \right)}^{{N_{\rm{r}}}}}\frac{{\left( {2{N_{\rm{r}}} + 1} \right)!!}}{{\left( {2{N_{\rm{r}}} + 2} \right)!!}}\left[ {\frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}}} + \frac{1}{{\left( {{N_{\rm{r}}} - 1} \right){{\bar \gamma }_{{\rm{rd}}}}}}} \right]} \end{array} $ | (38) |
Then the average BER is approximated as
| $ {P_{\rm{e}}} \approx \frac{{{N_{\rm{t}}}}}{2}{\left( {\frac{2}{{{{\bar \gamma }_{{\rm{sd}}}}}}} \right)^{{N_{\rm{r}}}}}\frac{{\left( {2{N_{\rm{r}}} + 1} \right)!!}}{{\left( {2{N_{\rm{r}}} + 2} \right)!!}}\left[ {\frac{1}{{{{\bar \gamma }_{{\rm{sr}}}}}} + \frac{1}{{\left( {{N_{\rm{r}}} - 1} \right){{\bar \gamma }_{{\rm{rd}}}}}}} \right] $ | (39) |
With Eqs. (37) and (39), the asymptotically approximated BER expressions for Nr=1 and Nr≥2 are attained, respectively. It is shown that they have values close to the corresponding simulations under high SNR.
In what follows, we will give the analysis of the diversity gain. Let Ps=r1Pt, Pr=r2Pt, where r1+r2=1 and r1, r2∈[0, 1], we can obtain
| $ \begin{array}{*{20}{c}} {{P_{\rm{e}}} \approx \frac{{3{N_{\rm{t}}}}}{{8{{\bar \gamma }^2}}}\frac{{{r_1} + \tau }}{{{r_1}\tilde \delta _{{\rm{rd}}}^2\tau }}\left[ {\frac{{{r_1} + \tau }}{{{r_1}\tilde \delta _{{\rm{sr}}}^2\tau }} + } \right.}\\ \left. {{\frac{{{r_2} + \tau }}{{{r_2}\tilde \delta _{{\rm{rd}}}^2\tau }}\left( {\ln \left( {\frac{{2{r_2}\delta _{{\rm{rd}}}^2\tau \bar \gamma }}{{{r_2} + \tau }}} \right) + \psi \left( 1 \right) - \frac{7}{6}} \right)}} \right] \end{array} $ | (40) |
| $ \begin{array}{*{20}{c}} {{P_{\rm{e}}} \approx \frac{{{2^{{N_{\rm{r}}} - 1}}{N_{\rm{t}}}}}{{{{\bar \gamma }^{{N_{\rm{r}}} + 1}}}} \cdot \frac{{\left( {2{N_{\rm{r}}} + 1} \right)!!}}{{\left( {2{N_{\rm{r}}} + 2} \right)!!}}{{\left( {\frac{{{r_1} + \tau }}{{{r_1}\tilde \delta _{{\rm{sd}}}^2\tau }}} \right)}^{{N_{\rm{r}}}}} \cdot }\\ {\left( {\frac{{{r_1} + \tau }}{{{r_1}\tilde \delta _{{\rm{sr}}}^2\tau }} + \frac{1}{{{N_{\rm{r}}} - 1}} \cdot \frac{{{r_2} + \tau }}{{{r_2}\tilde \delta _{{\rm{rd}}}^2\tau }}} \right)} \end{array} $ | (41) |
With the results above, we can evaluate the diversity order Gd, which is an important error performance indicator. Gd is defined as the slope of average BER curve for average SNR approaching infinity, and can be derived as [19]
| $ {G_{\rm{d}}} = \mathop {\lim }\limits_{\bar \gamma \to \infty } \left[ { - \frac{{\log \left( {{P_{\rm{e}}}} \right)}}{{\log \left( {\bar \gamma } \right)}}} \right] = {N_{\rm{r}}} + 1 $ | (42) |
Therefore, with the estimation error modeled as the decreasing function of SNR, the AF-SSK system will obtain the diversity order of Nr+1. As a result, the system performance will become better as the Nr increases.
4 Simulation ResultsIn this section, the BER performance of the cooperative AF-SSK system with imperfect channel estimation over Rayleigh channel is assessed by using the derived theoretical expressions and computer simulations. The number of transmit antennas at the source, Nt=2 or 4, and the path-loss exponent α=3. dsd, dsr and drd are the normalized distance for source-to-destination link, source-to-relay link and relay-to-destination link, respectively, and dsd:dsr:drd=1:0.5:0.5. The order of the polynomial Np in Eq.(9) is 5, and Ps=Pr=Pt/2. The variance of estimation error σ2esd=σ2esr=σ2erd=σe2. The simulation results are realized by Monte Carlo method.
In Fig. 2, we plot the average BER of AF-SSK system with estimation errors for different receive antennas, where Nr=1, 2, Nt=2. The variance of estimation error is given by
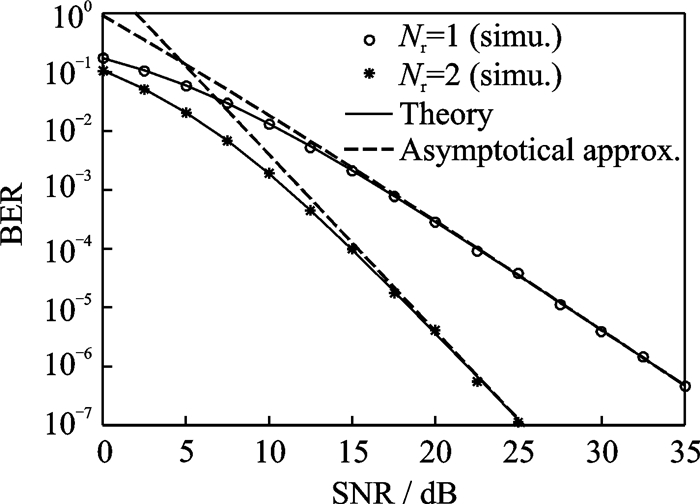
|
Fig. 2 Average BER of AF-SSK system with different receive antennas (Nt=2) |
Fig. 3 illustrates the BER performance of AF-SSK system with different receive antennas in the presence of imperfect estimations, where Nr=1, 2, and Nt=4. As shown in Fig. 3, the results similar to Fig. 2 can be found. Namely, the system with Nr=2 has better performance than that with Nr=1 because the former has larger diversity order than the latter. Moreover, the theoretical BERs can match the corresponding simulated ones, only small performance gap is observed at very low SNR. Besides, the approximated BERs are also close to the simulations at large SNR. All these results further show that the derived theoretical expressions are valid, and can provide good performance evaluation for the AF-SSK system under imperfect channel information.

|
Fig. 3 Average BER of AF-SSK system with different receive antennas (Nt=4) |
Fig. 4 shows the theoretical results and simulations of the average BER of AF-SSK system with different estimation errors. The number of transceiver antennas is Nr=Nt=2, and the variances of estimation errors are 0,

|
Fig. 4 Average BER of AF-SSK system with different estimation error variances |
5 Conclusions
Considering imperfect estimation information in practice, we have investigated the performance of cooperative AF-SSK system over Rayleigh fading channel. In the presence of estimation errors, the PDFs and MGFs of the effective SNR are respectively derived for the performance analysis. Based on this, closed-form average BER and the corresponding asymptotical BER are also deduced. Using the asymptotical BER, the diversity order is analyzed. As a result, the AF-SSK system can achieve the diversity order of Nr+1. Simulation results illustrate that the derived theoretical BERs can match well with the corresponding simulations for imperfect estimation information, and thus the correctness and effectiveness of theoretical analysis are validated. Thereby, the system performance can be evaluated well. Considering that the SM is the extension of SSK, in the future works, we will study the performance of the cooperative SM system with AF in the presence of channel estimation error so that the corresponding system performance can be well analyzed.
AcknowledgementsThis work is supported by the National Natural Science Foundation of China (Nos. 61601220, 61172077), the Foundation of Graduate Innovation Center in NUAA (No. kfjj20170410), the Fundamental Research Funds for the Central Universities, the Open Research Fund of National Mobile Communications Research Laboratory of Southeast University (No. 2017D03), and the Six Talent Peaks Project of Jiangsu Province (No. 2015-DZXX-007).
| [1] |
NOSRATINIA A, HUNTER T E, HEDAYAT A. Cooperative communication in wireless networks[J]. IEEE Communications Magazine, 2004, 42(10): 74-80. DOI:10.1109/MCOM.2004.1341264 |
| [2] |
ZHANG S W, YANG F F, TANG L. Joint iterative decoding for network-coding-based multisource LDPC-coded cooperative MIMO[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 31(4): 420-430. |
| [3] |
YANG P, DI RENZO M, XIAO Y, et al. Design guidelines for spatial modulation[J]. IEEE Communications Surveys & Tutorials, 2015, 17(1): 6-26. |
| [4] |
DI RENZO M, HAAS H, GRANT P M. Spatial modulation for multiple-antenna wireless systems:A survey[J]. IEEE Communications Magazine, 2011, 49(12): 182-191. DOI:10.1109/MCOM.2011.6094024 |
| [5] |
JEGANATHAN J, GHRAYBE A, SZCZECINSKI L. Space shift keying modulation for MIMO channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(7): 3692-3707. DOI:10.1109/TWC.2009.080910 |
| [6] |
MESLEH R, IKKI S S, AGGOUNE E M. Performance analysis of space shift keying (SSK) modulation with multiple cooperative relays[J]. Eurasip Journal on Advances in Signal Processing, 2012, 201: 1-10. |
| [7] |
MESLEH R, IKKI S S. Space shift keying with amplify-and-forward MIMO relaying[J]. Transaction on Emerging Telecommunications Technologies, 2015, 26(4): 520-531. DOI:10.1002/ett.v26.4 |
| [8] |
SHU F, WA NG, Z W, CHEN R Q, et al. Two high-performance schemes of transmit antenna selection for secure spatial modulation[J]. IEEE Transactions on Vehicular Technology, 2018, 67(10): 1-5. DOI:10.1109/TVT.2018.2872207 |
| [9] |
ALTIN G, BASAR E, AYGOLU U, et al. Performance analysis of cooperative spatial modulation with multiple-antennas at relay[C]//IEEE International Black Sea Conference on Communications and Networking. Varna, Bulgaria: IEEE, 2016: 1-5.
|
| [10] |
ALTIN G, AYGOLU U, BASAR E, et al. Multiple-input-multiple-output cooperative spatial modulation systems[J]. IET Communications, 2017, 11(15): 2289-2296. DOI:10.1049/iet-com.2016.0977 |
| [11] |
MESLEH R, IKKI S S. Analysis of Cooperative Communication spatial modulation with imperfect channel estimation[C]//IEEE 24th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). London, UK: IEEE, 2013: 2023-2027.
|
| [12] |
AFANA A, NGATCHED T M N, DOBRE O A, et al. Cooperative DF cognitive radio networks with spatial modulation with channel estimation errors[C]//IEEE Wireless Communications and Networking Conference (WCNC). San Francisco, USA: IEEE, 2017: 1-5.
|
| [13] |
NAIDOO N R, XU H J, QUAZI T A. Spatial modulation:Optimal detector asymptotic performance and multiple-stage detections[J]. IET Communications, 2011, 5(10): 1368-1376. DOI:10.1049/iet-com.2010.0667 |
| [14] |
HAN S, AHN S, OH E, et al. Effect of channel-estimation error on BER performance in cooperative transmission[J]. IEEE Transaction on Vehicular Technology, 2009, 58(4): 2083-2088. DOI:10.1109/TVT.2008.2007644 |
| [15] |
ROY S, FORTIER P. Maximal ratio combining architectures and performance with channel estimation based on a training sequence[J]. IEEE Transactions on Wireless Communications, 2004, 3(4): 1154-1164. DOI:10.1109/TWC.2004.828022 |
| [16] |
ABRAMOVITZ M, STEGUN I A. Handbook of mathematical functions[M]. New York: Dover Publications, 1970.
|
| [17] |
GRADSHTEYN I S, RYZHIK I M. Table of integrals, series, and products[M]. 7th ed. San Diego: Academic Press, 2007.
|
| [18] |
PROAKIS J G. Digital communications[M]. 4th ed. New York: McGraw-Hill, 2001.
|
| [19] |
ZHENG L, TSE D. Diversity and multiplexing:A fundamental tradeoff in multiple antenna channels[J]. IEEE Transactions on Information Theory, 2003, 49(5): 1073-1096. DOI:10.1109/TIT.2003.810646 |
 2018, Vol. 35
2018, Vol. 35


