2. General Control Department, Space Transportation Technology CO. Ltd., Beijing 100176, P. R. China;
3. Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, P. R. China
Nomenclature
D=Diameter of the nose
L=Model length
L1=First cone length
L2=Wing-body length
Φ1=First cone base diameter
Φ2=Wing-body base diameter
S=Span of the triangular wings
χ=Leading edge swept angle of the wing
P=Static pressure
P0=Freestream total pressure before shock wave
P0f=Freestream total pressure behind shock wave
P0j=Jet total pressure
Pj=Jet static pressure
P∞=Inflow static pressure
T∞=Inflow static temperature
Ma=Inflow Mach number
Maj=Jet Mach number
Re=Reynolds number based on the model length
α=Angle of attack
CD=Drag force coefficient
CL=Lift force coefficient
Xcp=Pressure center coefficient
k=Lift-to-drag ratio
0 IntroductionTo increase the gliding range, a lifting-body shape is usually employed for hypersonic vehicle design because of high lift-to-drag characteristics. Considering the installation of system components and thermal protection, the nose of the vehicle is blunt, which causes a strong normal shock at hypersonic speeds. The strength of the shock is proportional to the flight Mach number. The nose drag force induced by the shock wave is responsible for more than 30% of the total drag force at hypersonic speeds, and a 1% overall drag reduction would translate to a 5%—10% drag increase in payload[1]. When supersonic/hypersonic vehicles cruise in the region of near-space, they will withstand heavy heat-load at the nose, accompanied with huge drag force induced by the shock wave. Therefore, it is required to design the drag reduction and the thermal protection system properly.
At hypersonic speeds, the wave drag can be reduced by various methods such as aerospikes ahead of the blunt body[2], counterflowing jet in the stagnation zone[3] and energy deposition along the stagnation streamline[4, 5]. An aerospike is used in launching vehicles and missiles as a mature drag reduction technology. The aerospike increases the lift-to-drag ratio and offers high volumetric efficiency by using a blunt body instead of a slender body. However, at high velocities, the spike suffers from serious thermal condition which limits aerospikes to be used on hypersonic vehicles which need to fly long distance. Energy deposition produces drag reduction while it also increases heat transfer to the vehicles. These drawbacks of the two methods mentioned above provide motivation to study the method of counterflowing jet. Using counterflowing jet, the mass injection technique avoids the problem of a physical spike being heated and ablated as well as reduces the overall drag and heat transfer to the body. At the same time, stealth performance is essential for the design of hypersonic aircrafts in the future, which means that the counterflowing jet is better than spike, since the counterflowing jet would not install an extra geometry on the vehicle.
In the 1960s, Finley[6] performed a series of experiments in which a jet injected air from an orifice at the nose of a body in supersonic flow to oppose the mainstream and developed an analytical model of the flow. The experiments suggested that the aerodynamic features of the steady flow depended primarily on both the jet flow-force coefficient and the jet Mach number on its exit plane. Charczenko and Hennessey[7] found that the pressure decreases as the freestream Mach number increases with a constant jet thrust. As one of the most obvious features of counterflowing jet, shock bifurcation was discovered by computational and experimental studies[8] side-by-side. Shang et al.[9-11] focused on the pressure ratio and described the counterflowing jet phenomenon. They found that the shock structures of the counterflowing jet have two distinct dynamic states[12]. At the bifurcation point, the total aerodynamic force (including the base drag, skin-friction drag, wave drag, and the reverse thrust of the counterflowing jet) reaches the minimum value. Farr et al.[13] described the long penetration mode (LPM) supersonic under-expanded counterflowing jet phenomenon. Evidences from experiments and computational fluid dynamics (CFD) analysis of LPM indicated that acoustics feedback and fluid interaction seen in LPM are analogous to the aeroacoustics interactions seen in screech jets. A numerical study of the influence of a counterflowing jet located at the central point of a blunt body in Ma=6.5 at 30 km altitude[14] showed a wave drag reduction of 55% due to the forward-facing jet. Various pressure ratios were also investigated by Shah et al.[15], Venukumar et al.[16] and Fomichev et al.[17], who concluded that the drag reduction can be expressed as a function of relative mass flow ratio under kinds of freestream conditions. Josyula et al.[18] experimentally investigated the potential applications of a counterflowing jet to assess the performance improvements on aerospace vehicles and found that 30%—50% drag reduction could be achieved.
In recent years, in order to enhance the drag reduction effect, researchers also studied several combinations including the combination of counterflowing jet and aerospike[19-22], the combination of counterflowing jet and energy deposition[23], and the combination of counterflowing jet and forward-facing cavity[24, 25]. Numerical results showed that the drag reduction grows with the increase of the length-to-diameter ratio of aerospike and the jet pressure ratio. The energy deposition upstream can enhance stability and penetration of the forward injection jet significantly. In addition to researches on hemispherical head for drag reduction, the same effect of counterflowing jet has been found on hypersonic vehicles such as blunt cone reentry capsule[26-30], two blunt cone flare bodies[31], slender-body configurations[32-34] and waverider[35]. Numerical results showed about 16%—42% drag reduction for 60° apex-angle blunt module[36], and lift-to-drag ratio could be improved 4%—5% for blunt waverider in the hypersonic flow.
This paper presents an investigation on drag reduction effects of counterflowing jet on a double-cone-wing lifting-body vehicle at hypersonic speeds. The influence of different jet pressure ratios on the drag performance and the aerodynamic characteristics of the vehicle at different angles of attack are studied by numerical simulations. This is the first time that drag reduction using a counterflowing jet method has been investigated on a lift-body-wing configuration at hypersonic speeds. The research also reveals the lift and drag characteristics of hypersonic vehicle with counterflowing jet around the cruise flight angles of attack.
1 Numerical Method 1.1 Computational modelThis study uses a general hypersonic model which can be axially divided into three parts, including the nose, the first cone and the wing-body. The overall length of the model is 3 000 mm. The first cone has a base diameter of 300 mm and length of 700 mm. The wing-body has a base diameter of 450 mm and length of 2 300 mm. The span of the triangular wings is 1 500 mm which is the same length as the wing-body and the leading edge swept angle of the wing is 75.6°. The nose of the model is a spherical cap with a diameter of D=100 mm. In order to explore the drag reduction effects of counterflowing jet on the nose part of the lifting-body model, a circular-shaped jet with a diameter of 0.1D is introduced at the nose center and the medium of the counterflowing jet is air. The hypersonic vehicle flies at an altitude of 40 km and Ma= 8. In order to investigate the jet effects, a simulation without the counterflowing jet is also conducted as the baseline model. The geometry of the model with the jet nozzle is shown in Fig. 1.
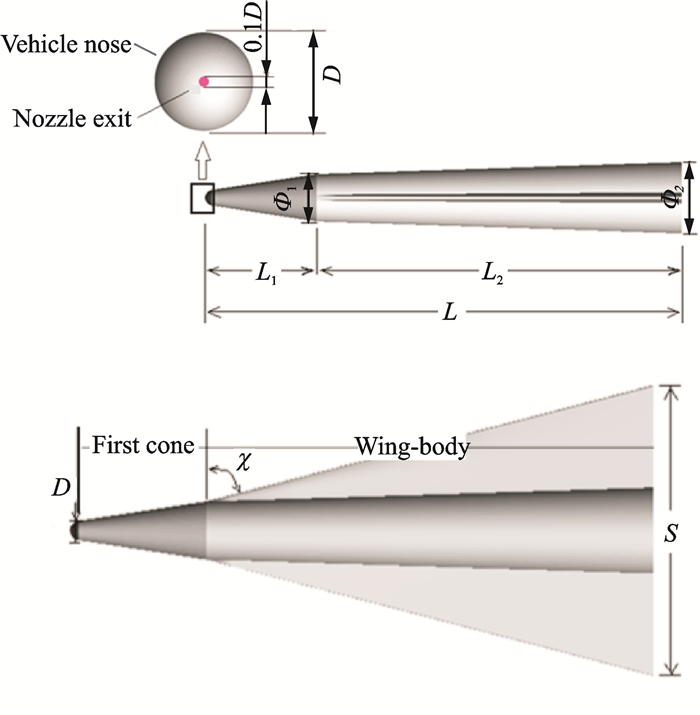
|
Fig. 1 Lifting-body model with counterflowing jet |
At an altitude of 40 km, the static pressure and static temperature of the freestream are 287 Pa and 250 K, respectively. Accordingly, the length Reynolds number is Re=1.9×106. At this Reynolds number, the laminar flow can be assumed[37]. The jet is a cold one, which is 284.2 K.
The conditions for the jet were found by Romeo and Sterrett[38], who observed two distinct types of jet interaction and judgment transition between the two flow states with the jet pressure ratio (PR), which is defined as
| $ {\text{PR}} = {P_{0{\text{j}}}}/{P_{0{\text{f}}}} $ | (1) |
The jet PR is proved to be one of the most important parameters for the flow phenomena which is created by the interaction between the counterflowing jet and the incoming air. The flow conditions for the computations performed are summarized in Table 1.
| Table 1 Flow condition of free stream and counterflowing jet |
In this study, the three-dimensional, laminar, unsteady Navier-Stokes equations are employed to do the simulations, using the density density-based solver in FLUENT. The commercial software is using cell-centered finite-volume-method. The spatial numerical scheme is Roe scheme coupled with second-order upwind scheme and the time marching scheme is implicit. With the suitable under-relaxation factors, the Courant-Friedrichs-Levy (CFL) number is 0.01 to avoid divergence at the beginning steps, then CFL is increased to 0.3, making sure the progress of convergence is stable and the simulation is not too slow. The simulations are considered convergent when all the residuals are reduced with five orders. Non-slip and adiabatic boundary conditions are set for the walls. It is assumed that the air is calorically perfect gas. The viscosity coefficient is obtained by the Sutherland equation. The incoming freestream boundary is pressure-far-field and the inlet of the counterflowing jet is velocity inlet. For the outlet boundary condition, all the physical variables are extrapolated from the internal cells because the outlet is far from the vehicle and the flow should be supersonic at the outlet boundary. 5% turbulence was set for the free stream flow. The k-ω turbulent model was used for the present simulation.
1.2 Computational gridsTo simulate the flow fields, a hybrid grid is generated by Gridgen to capture the complex flow around the model. The mesh in front of the nose is equivalently geometric scaled unstructured mesh, which has been previously shown to simulate the jet flow well[39]. The model wings and body employ multi-block-structured mesh which is highly concentrated close to the wall surfaces to ensure the accuracy of the numerical simulation. The mesh is shown in detail in Fig. 2. The height of the first cell from the wall is 5×10-5 m to resolve the boundary layer near the wall. The final mesh has 15.07 million cells. The aerodynamic coefficients and the position of pressure center are based on the reference length of 3 m and reference area of 0.2 m2, which are the length of the main body and the area of the model base, respectively. The original point is set at the central point of the nose surface.
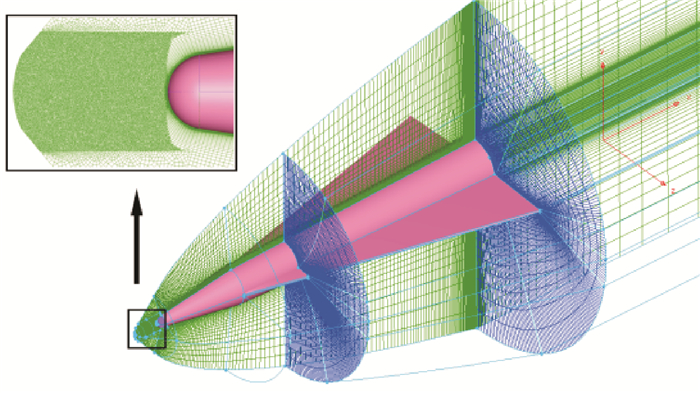
|
Fig. 2 Computation area and mesh distribution |
1.3 Validation
To validate the numerical solver, a three-dimensional axisymmetric 2.6%-scale Apollo capsule model with 0° angle of attack is used. The same model was studied througth experiments by Daso et al.[29]. The forebody of the model is a spherical cap with a curvature radius of 121.92 mm and a base diameter of 101.6 mm. The shoulder radius is 5.08 mm. The inverted cone angle is 32.27°. The jet nozzle exit is positioned on the center of the nose surface and the model has a diameter of 12.7 mm.
The boundary conditions are given as follows. For the pressure far field, a uniform free-stream condition at the upstream is specified, which is Ma=3.48, P∞=4 201 Pa, T∞=94.2 K. The jet total temperature is 284.2 K at the jet exit, and the jet Mach number is 2.94 at the same location.
The supersonic flow field in front of the nozzle exit is simulated and compared with the data of Ref.[39]. As shown in Fig. 3, the shock stand-off distance of the flow agrees well with the reference data. Fig. 4 shows a qualitative comparison of the Schlieren picture and the CFD prediction of the interaction with a free-stream Ma=3.48 and Ma=2.94, and a jet flow rate of 0.215 kg/s. This complex flow field constitutes a new displacement shape with the jet pushing the bow shock away from the body surface. The Mach disk is clearly observed. As the fluid from the jet runs in the opposite direction of free flow, conical shear layer is formed, which leads to the formation of a recirculation region.The shock structure and flow field shape are consistent with the experiment result of the Schlieren picture.The results prove that the numerical method can be used to obtain the aerodynamic characteristics of the model with counterflowing jet.
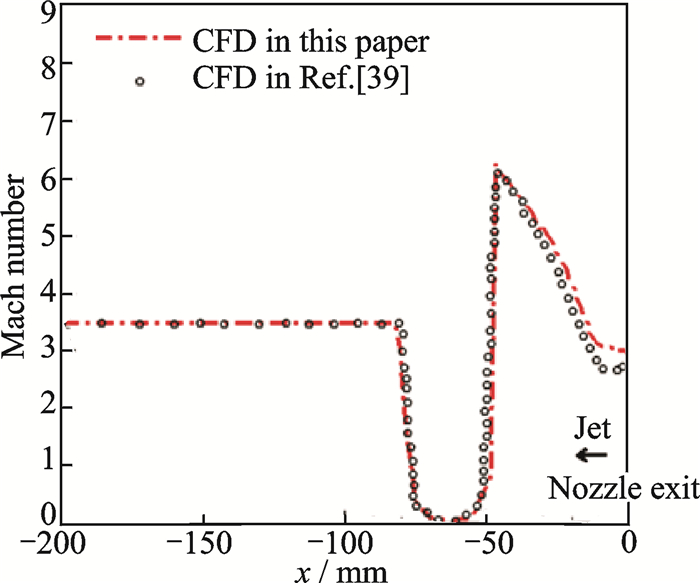
|
Fig. 3 Mach number distribution along the jet centerline |

|
Fig. 4 Comparison between exp Schlieren picture (top) and CFD total density gradient contour (bottom) |
2 Results and Discussion 2.1 Flow field structure
The density contour on the symmetry plane is shown in Fig. 5 to compare the flow structures of baseline model and the model with counterflowing jet of PR=3.91 at Ma=8 and angle of attack of 6°. It shows that the shock shape in the front of the nose is changed from a strong bow shock into a weak oblique shock by adding a counterflowing jet. This is the reason why a counterflowing jet can reduce the wave drag of the high-speed vehicles.
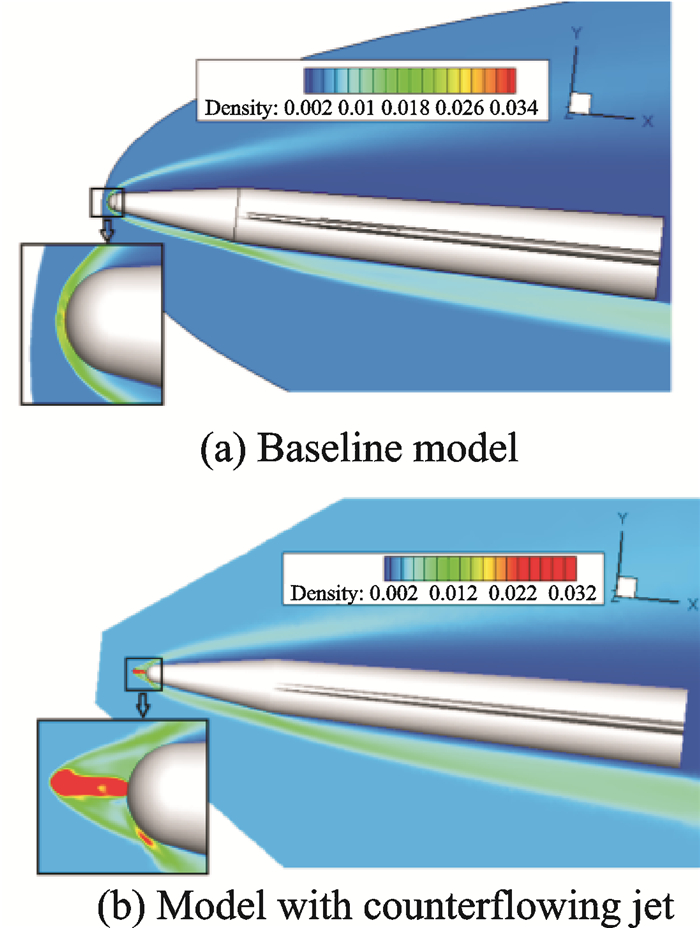
|
Fig. 5 Density contour of model on the symmetric plane (Ma=8, α=6°) |
Fig. 6 shows the effects of different pressure ratios on the flow field in front of the nose by displaying Mach number and pressure distributions. The Mach number distributions along with the axial centerline are shown in Fig. 7. As shown in Fig. 6(a), the jet flow is retained within the boundary layer and lacks sufficient momentum to disturb the bow shock at PR=1.02. The flow field is similar to that of the model with no jet in Fig. 5(a). As the PR is increased, the jet flow begins to interact with the bow shock. The shock standoff distance increases proportionally until the distance reaches the maximum displacement at PR=3.91, as shown in Fig. 6(c). An LPM region is formed when the flow field is dominated by a diamond-pattern shock structure, which creates a new oblique shock structure ahead of the bow shock. As the PR increases further, the shock standoff distance rapidly decreases, as shown in Fig. 6(d), and the entire flow structure collapses back to short penetration mode(SPM). It is necessary to point out that, with the further increase of the PR, as shown in Fig. 6(f), the shock standoff distance increases again, and shows an LPM-like flow structure.

|
Fig. 6 Flow field in front of the nose with counterflowing jet |
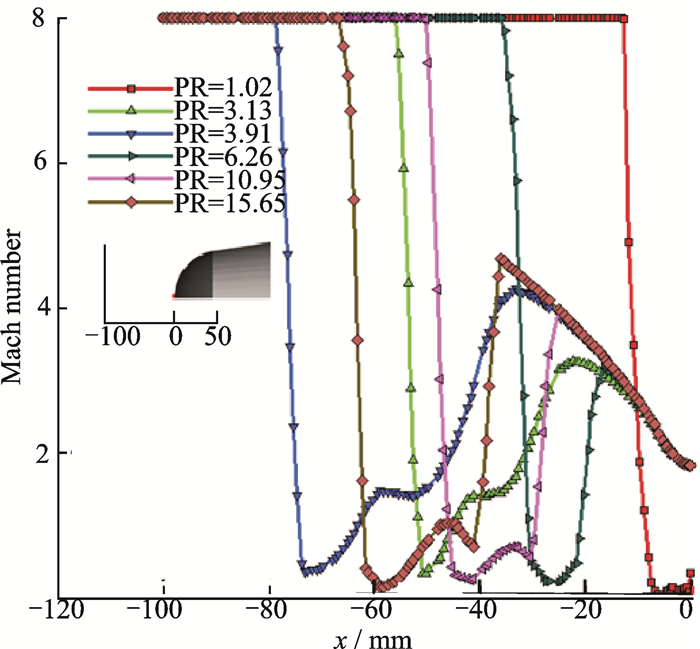
|
Fig. 7 Mach number distributions with different PR |
It can be concluded that LPM occurs at the low value of PR while SPM occurs at a relative high value of PR. Prior studies on counterflowing jets from the orifice at the central point of a hemispherically blunted body in supersonic and hypersonic flow[40-42] indicated that the transition from LPM to SPM occurred at a fixed PR. This critical value is found to be between 3.91 and 6.26 in our research.
The non-dimensional static pressure distributions on the surface of the nose with different PR are given in Fig. 8. It reveals that the pressures on the surfaces with counterflowing jet in the recirculation region are obviously much lower than the stagnation-region pressures of the baseline model.
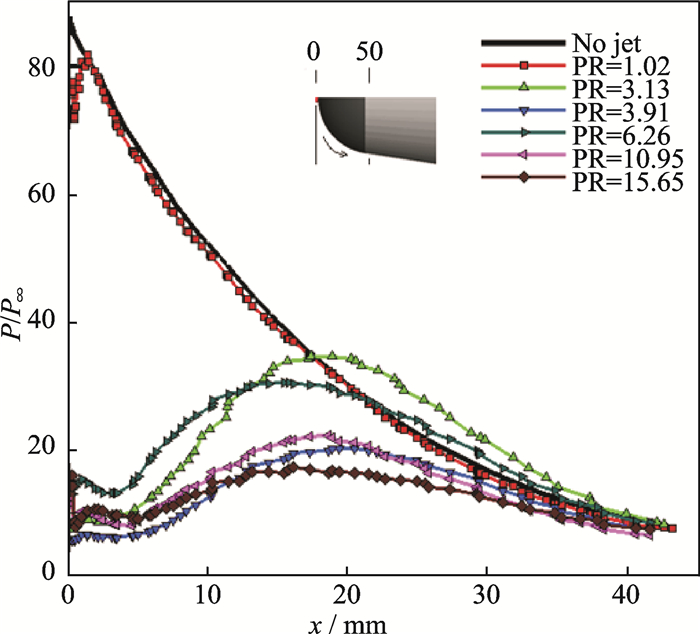
|
Fig. 8 Static pressure distributions on the surface of the nose |
With the increase of PR from 1.02, the static pressure level on the nose surface decreases gradually until PR=3.91 where the static pressure level reaches the smallest value. After that, the static pressure rises sharply because the flow mode changes from LPM to SPM, then it sustains a gradually decreasing tendency with the increase of PR and reaches the minimum value at PR=15.65.
2.2 Influence of reverse thrust on drag of noseWhen the modified drag is being calculated on the nose, the reverse thrust is added to the axial component of the pressure which is integrated over the nose surface. Djet is the total drag with jet including the drag penalty of the counterflowing jet.D0 is the drag of the nose surface and D is the non-dimensional drag that is divided by the drag of nose without jet. To evaluate the overall performance, the drag coefficients are time-averaged values. The drag coefficients on the nose surface variation with PR is given in Fig. 9.
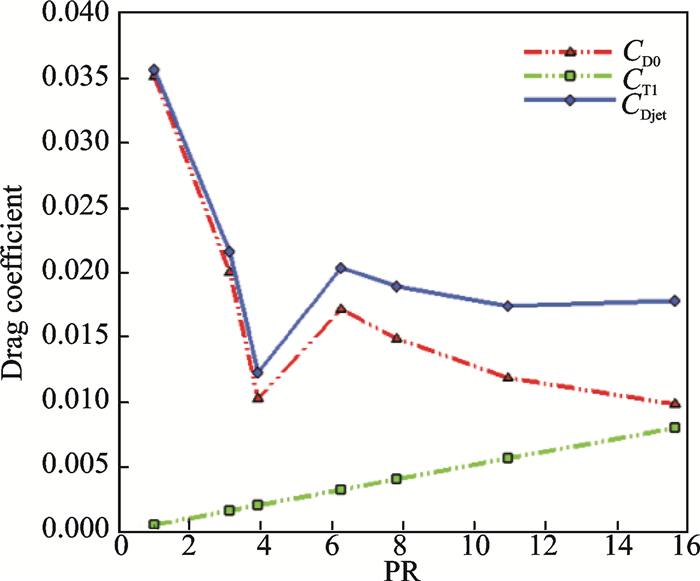
|
Fig. 9 Variation of drag coefficients with PR |
The function of calculating the reverse thrust which produces counterflowing jet is
| $ {T_{\text{j}}} = \dot m{V_{\text{j}}} + {A_{\text{j}}}\left( {{P_{\text{j}}}-P} \right) $ | (2) |
where
As shown in Fig. 9, the reverse thrust of the counterflowing jet linearly grows with the increase of PR, meanwhile, the drag of the nose surface overwhelms completely the reverse thrust in a large part of the PR range. With the increase of PR, the drag falls continuously until PR=3.91. Beyond this value, the drag increases sharply and then sustains a continuously drop with a shallow slope. Because of the slender effective body shape created by LPM jet, the drag reduction efficiency of LPM jet is better than SPM jet.
As shown in Table 2, in the transition region from LPM to SPM, the maximum drag reduction is 66%. However, for the SPM conditions, the drag reduction varies from 43% to 52%, depending on the jet total pressure. If only judging from the drag force of the nose, the minimum drag value is obtained at PR=15.65. However, considering the drag penalty of the jet, the maximum drag reduction is obtained at PR=3.91, indicating that the reverse thrust produced by the jet should be added in the total drag for a realistic simulation.
| Table 2 Drag force of the nose |
2.3 Impact of angle of attack on drag of model
Hypersonic vehicles usually cruise with a small angle of attack[43]. This angle is around the maximum lift-to-drag ratio angle, which is around 6°—8° for the majority of lifting-body vehicles[44]. With a typical angle of attack, there should be an obvious influence on the drag reduction effect. Lu and Liu[45] numerically proved that, besides the heavy heat flux problem, the drag coefficient of the nose with the counterflowing jet also increases with the increase of angle of attack. Thus, aerodynamic characteristics are researched to investigate the drag reduction influence of the lifting-body model at flying angles of attack.
The Mach number distributions of the model with jet of PR=3.91 at variable angles of attack are shown in Fig. 10. As shown in the figures, the flow structure is symmetric in the Y direction at an angle of attack of 0°. The distributions of the shock structure and the shear layer are tilted when the angle of attack increases, but the LPM mode of the counterflowing jet is maintained until an angle of attack of 8°. The low pressure recirculation zone on the windward side becomes smaller as the angle of attack increases. An extra high pressure region is formed and the drag reduction effect of the counterflowing jet is weakened when the angle of attack is larger than 8°. It can be concluded that the drag reduction performance strongly depends on flying angle of attack. Based on the results of this study, if the geometric shape and PR are carefully designed, the effective application range of counterflowing jet method can cover the flying angle of attack.
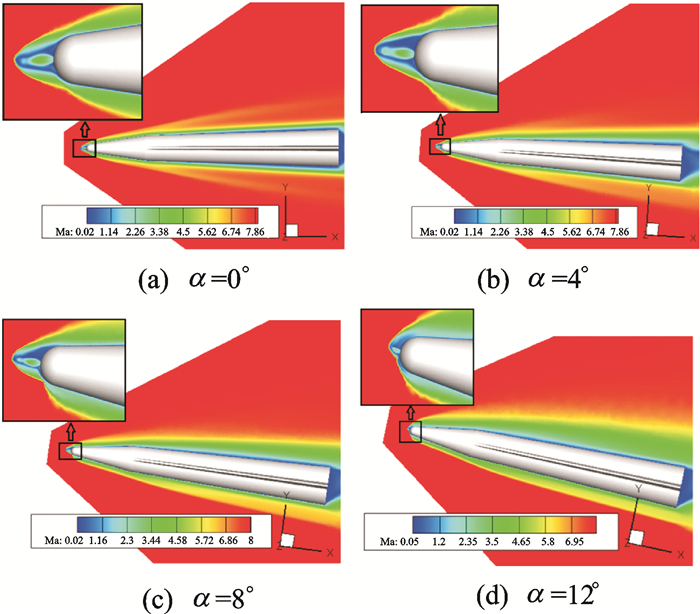
|
Fig. 10 Mach number contour of the model on symmetric plane and nose surface |
The variation of pressure drag coefficients CDP with the angle of attack is showed in Fig. 11. The no jet case is shown for a reference. The pressure drag of the nose without jet remains about the same as the increase of the angle of attack. By adding the counterflowing jet on the nose, the pressure drag decreases sharply due to the presence of the low pressure recirculation zone. With the increase of the angle of attack, the recirculation zone decreases, which result in the rapid increase of pressure drag.
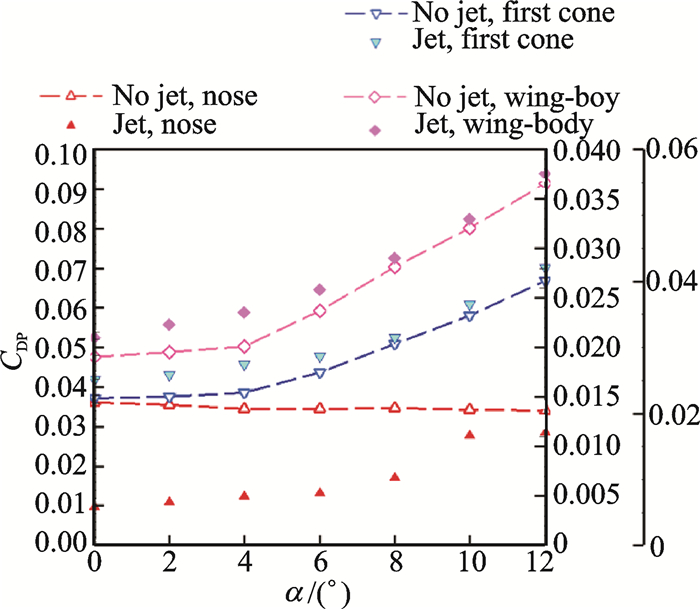
|
Fig. 11 Pressure drag coefficients variation with the angle of attack |
The pressure drag of the first cone and wing-body increases linearly with increasing angle of attack. Compared with the baseline model, the pressure drag of the model with the jet is slightly larger. The gap between them gradually narrows with the increase of the angle of attack and the values are almost the same when the angle of attack is greater than 8°, which means that the counterflowing jet on the nose has almost no effect on the pressure distribution of the first cone and wing-body.
The variation of skin friction drag coeffieients CDV with the angle of attack is showed in Fig. 12. Skin friction drag of wing-body with and without counterflowing jet is nearly the same. It indicates that the effect of counterflowing jet on the wing-body is very small, but skin friction drag of the nose with counterflowing jet is significantly smaller than that of the no jet case. As shown in Fig. 10, the recirculation zone is largely responsible for skin friction drag reduction. The recirculation causes the flow to move upstream along the body, causing a decrease in the total skin friction drag. At the same time, with the jet fluid being added into the flow, the temperature of the nose surface can be brought below that of the free stream, which drastically reduces the effect of viscosity around the nose. The maximum value of skin friction drag reduction of the nose and first cone are 83.8% and 20.6%, respectively. Skin friction drag of the nose with counterflowing jet increases as the angle of attack increases and the drag reduction effect gradually decreases. When the angle of attack is greater than 8°, skin friction drag of the first cone with counterflowing jet is larger than that of the no jet case, which means the counterflowing jet has no beneficial effect on the first cone.
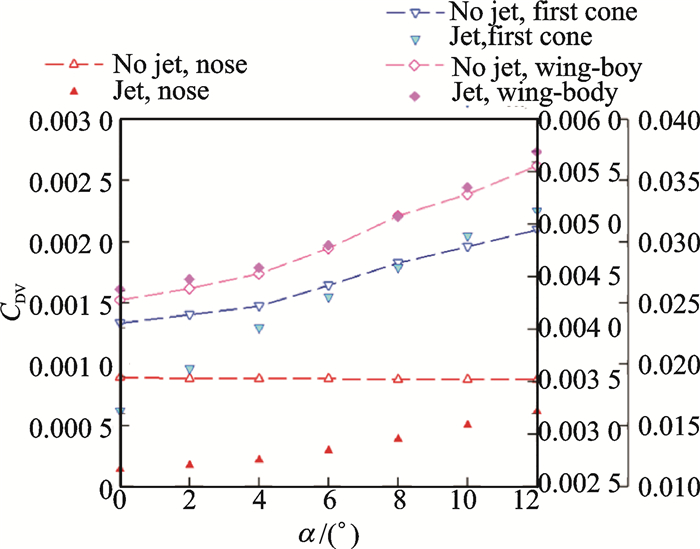
|
Fig. 12 Skin friction drag coefficients variation with the angle of attack |
To quantify the advantages of model with counterflowing jet, the aerodynamic characteristics are compared in Fig. 13. From Fig. 13(a), a drag reduction of 18.4% at α=0° can be obtained for model with the jet, but the drag beyond α=10° is almost the same as that obtained by the baseline model, which means that the counterflowing jet with proper PR can produce a relatively drag reduction within 8° for hypersonic lifting-body. The jet effectively improves the lift-to-drag ratio of the model, shown in Fig.13(b), and gains a better lift-to-drag ratio than the baseline model between 2°—10°. The lift-to-drag ratio is enhanced from 3.344 to 3.576 at α=6°, and the value increases by 7.0%. As shown in Fig. 13(c), it is interesting to note that the movement of the center of pressure decreases from 1.2% to 0.6% when the jet is used, which means that the rudder trim for flight phases is reduced, thereby reducing the trim drag of the pneumatic rudder.
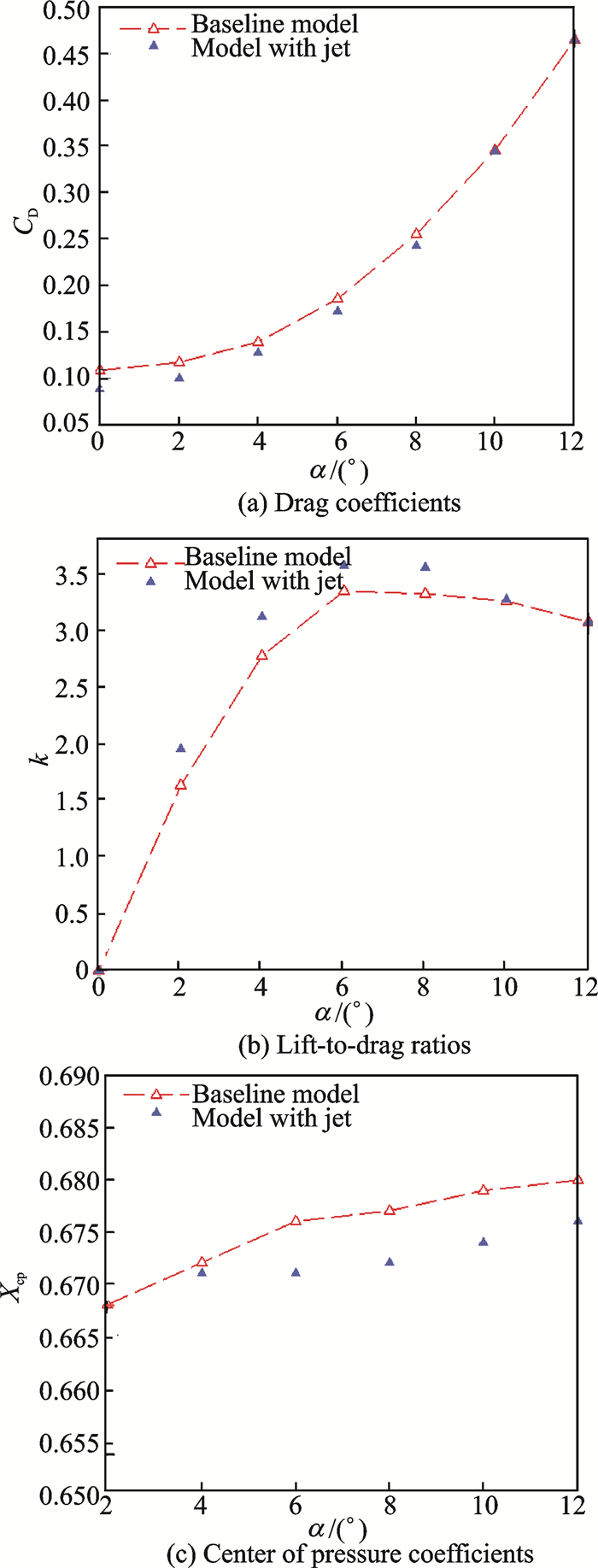
|
Fig. 13 Comparison of aerodynamic coefficients for the models with and without jet |
3 Conclusions
The drag reduction effect of supersonic counterflowing jet with different pressure ratios on the hypersonic lifting-body model at Ma=8 has been numerically investigated and a comparison has been made with the baseline case. Moreover, the influence of angles of attack on the drag reduction performance with certain PR conditions is discussed.
There are two flow modes in the studied range of PR, including LPM and SPM. LPM occurred at a lower value of PR while SPM occurred at a relatively high value of PR. The transition from LPM to SPM occurred at a fixed PR. This critical value obtained from this study is between 3.91 and 6.26. The counterflowing jet attains the maximum penetration into the shock layer to produce the slenderest displacement configuration at PR=3.91. Taking the reverse thrust into account, the maximum drag reduction of the nose is 66%.
The LPM mode of the counterflowing jet could be maintained below an angle of attack of 8°. The efficacious application range of counterflowing jet technology can cover the flying angle of attack for the model studied in this paper. The recirculation zone is responsible for the skin friction drag reduction. The counterflowing jet has no beneficial effect on the first cone when the angle of attack is greater than 8°. The drag reduction of the whole model is 8.8% at α=6° and the lift-to-drag ratio is 3.576, which is 7.0% better than that of the baseline model. The movement of the center of pressure decreases from 1.2% to 0.6% compared with the baseline model, providing better stability characteristics for lifting-body vehicles.
AcknowledgementsThis work was supported by the Aeronautics Science Foundation (No.20163252037), the China Postdoctoral Science Foundation (No.2017M610325), the Natural Science Foundation of Jiangsu Province (No.BK20170771), and Fundamental Research Funds for the Central Universities (No.NP2017202).
| [1] |
BUSHNELL D M. Shock wave drag reduction[J]. Annu Rev Fluid Mech, 2004, 36: 81-96. DOI:10.1146/annurev.fluid.36.050802.122110 |
| [2] |
AHMED M, QIN N. Drag reduction using aerodisks for hypersonic hemispherical bodies[J]. Journal of Spacecraft and Rockets, 2010, 47(1): 62-80. DOI:10.2514/1.46655 |
| [3] |
RONG Y, WEI Y, ZHAN R. Research on thermal protection by opposing jet and transpiration for high speed vehicle[J]. Aerospace Science and Technology, 2016, 48: 322-327. DOI:10.1016/j.ast.2015.11.014 |
| [4] |
SATHEESH K, JAGADEESH G. Effect of concentrated energy deposition on the aerodynamic drag of a blunt body in hypersonic flow[J]. Physics of Fluids, 2007, 19(3): 031701. DOI:10.1063/1.2565663 |
| [5] |
ERDEM E, KONTIS K, YANG L. Steady energy deposition at mach 5 for drag reduction[J]. Shock Waves, 2013, 23(4): 285-298. |
| [6] |
FINLEY P J. The flow of a jet from a body opposing a supersonic free stream[J]. Journal of Fluid Mechanics, 1966, 26(2): 337-368. DOI:10.1017/S0022112066001277 |
| [7] |
CHARCZENKO N, HENNESSEY K W. Investigation of a retrorocket exhausting from the nose of a blunt body into a supersonic free stream: TR TN D-751[R].USA: NASA, 1961.
|
| [8] |
ROCKWELL D, NAUDASCHER E. Self-sustained oscillations of impinging free shear layers[J]. Annual Review of Fluid Mechanics, 1979, 11(1): 67-94. DOI:10.1146/annurev.fl.11.010179.000435 |
| [9] |
SHANG J S, HAYES J, WURTZLER K, et al. Jet-spike bifurcation in high-speed flows[J]. AIAA Journal, 2001, 39(6): 1159-1165. DOI:10.2514/2.1430 |
| [10] |
SHANG J S, HAYES J, MENART J. Hypersonic flow over a blunt body with plasma injection[J]. Journal of Spacecraft and Rockets, 2002, 39(3): 367-375. DOI:10.2514/2.3835 |
| [11] |
SHANG J S, HAYES J, MILLER J, et al. Blunt body in electromagnetic hypersonic flow field[J]. Journal of Aircraft, 2003, 40(2): 314-322. DOI:10.2514/2.3095 |
| [12] |
SHANG J S. Validation of plasma injection for hypersonic blunt-body drag reduction: TR ADA415759[R].USA: NASA, 2003.
|
| [13] |
FARR R, CHANG C L, JONES J H, et al. On the comparison of the long penetration mode (LPM) supersonic counterflowing jet to the supersonic screech jet: AIAA 2015-3126[R].USA: AIAA, 2015.
|
| [14] |
MEYER B, NELSON H F, RIGGINS D W. Hypersonic drag and heat-transfer reduction using a forward-facing jet[J]. Journal of Aircraft, 2001, 38(4): 680-686. DOI:10.2514/2.2819 |
| [15] |
SHAH S B H, LU X Y. Computational study of drag reduction at various freestream flows using a counterflow jet from a hemispherical cylinder[J]. Engineering Applications of Computational Fluid Mechanics, 2010, 4(1): 150-163. DOI:10.1080/19942060.2010.11015306 |
| [16] |
VENUKUMAR B, JAGADEESH G, REDDY K P J. Counterflow drag reduction by supersonic jet for a blunt body in hypersonic flow[J]. Physics of fluids, 2006, 18(11): 118104. DOI:10.1063/1.2401623 |
| [17] |
FOMICHEV V P, FOMIN V M, KOROTAEVA T A, et al. Hypersonic flow around a blunted body with counterflow plasma jet[R]. Novosibirsk, Russia: Institute of Theoretical and Applied Mechance, 2002: 51-55.
|
| [18] |
JOSYULA E, PINNEY M, BLAKE W B. Applications of a counterflow drag reduction technique in high-speed systems[J]. Journal of Spacecraft and Rockets, 2002, 39(4): 605-614. DOI:10.2514/2.3850 |
| [19] |
HUANG W. A survey of drag and heat reduction in supersonic flows by a counterflowing jet and its combinations[J]. Journal of Zhejiang University SCIENCE A, 2015, 16(7): 551-561. DOI:10.1631/jzus.A1500021 |
| [20] |
GERDROODBARY M B. Numerical analysis on cooling performance of counterflowing jet over aerodisked blunt body[J]. Shock Waves, 2014, 24(5): 537-543. DOI:10.1007/s00193-014-0517-4 |
| [21] |
JIANG Z, LIU Y, HAN G, et al. Experimental demonstration of a new concept of drag reduction and thermal protection for hypersonic vehicles[J]. Acta Mechanica Sinica, 2009, 25(3): 417-419. DOI:10.1007/s10409-009-0252-8 |
| [22] |
HUANG W, LIU J, XIA Z. Drag reduction mechanism induced by a combinational opposing jet and spike concept in supersonic flows[J]. Acta Astronautica, 2015, 115: 24-31. DOI:10.1016/j.actaastro.2015.04.025 |
| [23] |
MARLEY C D, RIGGINS D W. Numerical study of novel drag reduction techniques for hypersonic blunt bodies[J]. AIAA Journal, 2011, 49(9): 1871-1882. DOI:10.2514/1.J050681 |
| [24] |
HUANG W, YAN L, LIU J, et al. Drag and heat reduction mechanism in the combinational opposing jet and acoustic cavity concept for hypersonic vehicles[J]. Aerospace Science and Technology, 2015, 42: 407-414. DOI:10.1016/j.ast.2015.01.029 |
| [25] |
SUN X W, GUO Z Y, HUANG W, et al. Drag and heat reduction mechanism induced by a combinational novel cavity and counterflowing jet concept in hypersonic flows[J]. Acta Astronautica, 2016, 126: 109-119. DOI:10.1016/j.actaastro.2016.04.022 |
| [26] |
KULKARNI V, REDDY K P J. Enhancement in counterflow drag reduction by supersonic jet in high enthalpy flows[J]. Physics of Fluids, 2008, 20(1): 016103. DOI:10.1063/1.2813042 |
| [27] |
KULKARNI V, HEGDE G M, JAGADEESH G, et al. Aerodynamic drag reduction by heat addition into the shock layer for a large angle blunt cone in hypersonic flow[J]. Physics of Fluids, 2008, 20(8): 081703. DOI:10.1063/1.2944982 |
| [28] |
KULKARNI V, REDDY K P J. Counterflow drag reduction studies for a blunt cone in high enthalpy flow[J]. International Journal of Hypersonics, 2010, 1(1): 69-76. DOI:10.1260/1759-3107.1.1.69 |
| [29] |
DASO E O, PRITCHETT V E, WANG T S, et al. Dynamics of shock dispersion and interactions in supersonic freestreams with counterflowing jets[J]. AIAA Journal, 2009, 47(6): 1313-1326. DOI:10.2514/1.30084 |
| [30] |
ZHOU C Y, JI W Y, XIE P. Numerical investigation on the drag and heat flux reduction of a supersonic reentry capsule with a counter-flow jet[J]. Information Technology Journal, 2012, 11(12): 1705-1713. DOI:10.3923/itj.2012.1705.1713 |
| [31] |
ARUNA S, ANJALIDEVI S P. Computational study on the influence of jet on reduction of drag over cone flare bodies in hypersonic turbulent flow[J]. Procedia Engineering, 2012, 38: 3635-3648. DOI:10.1016/j.proeng.2012.06.420 |
| [32] |
VENKATACHARI B S, CHENG G, CHANG C L, et al. Long penetration mode counterflowing jets for supersonic slender configurations-A numerical study: AIAA 2013-266[R].USA: AIAA, 2013.
|
| [33] |
VENKATACHARI B S, MULLANE M, CHENG G C, et al. Numerical experiments of counterflowing jet effects on supersonic slender-body configurations: TR NF1676L-20123[R].USA: NASA, 2015.
|
| [34] |
VENKATACHARI B S, MULLANE M, CHENG G C, et al. Numerical study of counterflowing jet effects on supersonic slender-body configurations: AIAA 2015-3010[R].USA: AIAA, 2015.
|
| [35] |
LI S B, WANG Z G, BARAKOS G N, et al. Research on the drag reduction performance induced by the counterflowing jet for waverider with variable blunt radii[J]. Acta Astronautica, 2016, 127: 120-130. DOI:10.1016/j.actaastro.2016.05.031 |
| [36] |
KANWAR S, SINGH M, JAISWAL S, et al. Numerical study on aerodynamic wave drag reduction by counterflow supersonic jet in hypersonic flow[J]. International Journal of Science and Research, 2013, 4(3): 181-187. |
| [37] |
KIMMEL R, ADAMCZAK D, JULIANO T, et al. HIFiRE-5 flight test preliminary results: AIAA 2013-0377[R].USA: AIAA, 2013.
|
| [38] |
ROMEO D J, STERRETT J R. Exploratory investigation of the effect of a forward-facing jet on the bow shock of a blunt body in a mach number 6 free stream: TR TN D-1605[R].USA: NASA, 1963.
|
| [39] |
VENKATACHARI B S, ITO Y, CHENG G, et al. Numerical investigation of the interaction of counterflowing jets and supersonic capsule flows: AIAA 2011-4030[R].USA: AIAA, 2011.
|
| [40] |
BUSHNELL D M, HUFFMAN J K.Forward penetration of liquid water and liquid nitrogen from the orifice at the stagnation point of a hemispherically blunted body in hypersonic flow: TR TM X-1493[R].USA: NASA, 1968.
|
| [41] |
FOMIN V M, MASLOV A A, SHASHKIN A P, et al. Flow regimes formed by a counterflow jet in a supersonic flow[J]. Journal of Applied Mechanics and Technical Physics, 2001, 42(5): 757-764. DOI:10.1023/A:1017984124396 |
| [42] |
CHEN L W, WANG G L, LU X Y. Numerical investigation of a jet from a blunt body opposing a supersonic flow[J]. Journal of Fluid Mechanics, 2011, 684: 85-110. DOI:10.1017/jfm.2011.276 |
| [43] |
DENG F, REN H, XIE F, et al. Research on wing-rudder interference of near-space hypersonic vehicle[J]. Journal of Astronautics, 2013, 34(6): 741-747. |
| [44] |
DENG F, REN H Y, LI X G, et al. Study on rudder effect of near-space hypersonic gliding vehicle with different control surfaces[J]. Acta Aerodynamica Sinica, 2014, 32(2): 264-270. |
| [45] |
LU H B, LIU W Q. Numerical investigation on properties of attack angle for an opposing jet thermal protection system[J]. Chinese Physics B, 2012, 21(8): 084401. DOI:10.1088/1674-1056/21/8/084401 |
 2018, Vol. 35
2018, Vol. 35


