In the past thirty years, international air transportation has changed dramatically since the beginning of the liberalization of the airline transportation. Besides, it becomes easier and easier to enter the air transportation market and the whole market is growing. The appearance of low-cost carriers has made some influence on the traditional carriers. To withstand market pressure and improve the route network, airlines find a new cooperation way-airline alliance.
The existing three major airline alliances have taken more than 70% of the airline transportation market. The formation of the airline alliance has a certain positive effect on the cost advantage, differentiation advantage and the specialized superiority. The development of the airline alliance can also reduce competition and improve flight frequency and service quality, etc. There are two main problems about the revenue management in airline alliance. First, we should guarantee the maximum revenue of the overall airline alliance. Second, we should ensure the fairness of revenue distribution among the members in airline alliance. This paper proposes a model to solve these two problems.
The study of code sharing route in airline alliance[1-2] shows that, the code sharing in complementary airline takes more revenue than that in parallel airline. And the higher proportion of code-sharing partners belongs to the same alliance, the higher revenue. In the same alliance, the higher degree of cooperation, the higher revenue. Boyd[3] first pointed out the concept of revenue management in airline alliance and proposed two common models for seat inventory control. One is block allocation, it contains hard block allocation and soft block allocation. The difference between two approaches is whether the number of seats is fixed. The other way is free sale method. In this approach, operating airline and marketing airline can share information about their own seats for sale. Jain[4] introduced the process of alliance revenue management, and the most important of which are the calculation of revenue distribution value and inventory control. Graf and Kimms[5-6] discussed the inventory control in single segment between two airlines in the use of options. Netessine and Shumsky[7] described the influence of horizontal and vertical competition to the total revenue in airline alliance. Grauberger and Kimms[8] discussed how to realize the maximization of single airline's revenue in alliance in the case of horizontal and vertical competition. Besides, they had used the concept of nucleolus in cooperative game theory to find a balanced solution to make the fair distribution of revenue within the alliance[9-11]. Hu[12] established a non-cooperative game to find a balance solution. Wright[13] proposed a Markov game to describe the alliance, with the dynamic marginal revenue which called as bid price to describe revenue allocation value. In order to propose airline's own true expected value in bargaining, there is a revenue distribution method based on the bargaining model[14]. Topaloglu[15] described a method of network revenue management based on the duality problem under incomplete information. But in his research, only considered the influence of single fare level, and didn't consider the influence of competence. Le meilong[16] and zhu bo[17] achieved the benefits of the airline through their transport control.
1 Assumptions of the ModelWe assume that an airline alliance contains many airline members that use code sharing. The route used as code sharing is called codeshare route. Codeshare route can be operated and sold by two or more airlines. There are two types of carriers in codeshare route, which are called as ticketing carriers and operating carriers. The former is in charge of selling, and the latter provides seats in an aircraft on the single flight leg. The route which is marketed and operated by only one carrier in alliance is called inter route.
The basic assumptions in the paper are as follows:
(1) There are many kinds of routes in alliance, such as codeshare routes and inter routes.
(2) Each route has two fare classes, and the demand of each fare class is independent and certain.
(3) There exists horizontal and vertical competition among airlines at the same time. The horizontal competition means two different airlines operating andmarketing the same itinerary. The horizontal competition means two airlines can join its own flight leg to form a new route in the market. The route maybe has the horizontal competition and the vertical competition at the same time.
(4) There are no team passengers. Overbooking, cancelling and no-shows are not considered in this study.
(5) The number of seats provided by airline members in the alliance is known, and the information about the fare class and corresponding demand can be shared between airlines in the same alliance.
(6) The different marketing airline has different level of demand in the same codeshare route.
(7) The fare of the same codeshare route can be different in different airlines.
2 Modelling and Analysis 2.1 Model under centralized mechanismK denotes the set of all airlines in alliance, and k∈K. L denotes the set of all segments operated by the airlines in alliance, and each segment is represented by i, i∈L. The flights operated by airline k is given by Lk. Let j denotes the OD route, and J is the set of all the routes. The routes associated with the airline k is Jk. f is used to denote different fare class, and f∈F. Since the existent of horizontal and vertical competence, CS represents the itineraries influenced by vertical competence, which means codeshare route, and the codeshare route associated with airline k is CSk. Besides, A represents the set of routes influenced by horizontal competence, and Ak denotes the routes in A which are operated by airline k. Let NAk denotes the routes that are not influenced by horizontal and vertical competence and operated by airline k, j∈CS∪A∪NA. Besides, since each flight maybe influenced by horizontal and vertical competence simultaneous, there may be an intersection between CS and A.
aij is 0-1 variable, aij=1 if route j has flight leg i. Otherwise, aij =0.cik denotes the number of seats provided by airline k in flight leg i. βjk, j∈CS∪A, k∈K is also 0-1 variable, and βjk=1, if the route of airline k is influenced by horizontal or vertical competence. Otherwise, βjk=0. fjfk denotes the price of fare class f when route j is operated by airline k. Djfk represents the demand of f fare class in route j that is operated by airline k. The sharing proportion of revenue in codeshare route j allocated to airline k is αjk. pjfk denotes the revenue in codeshare route jof fare class f that allocated to airline k, and
| $ Z = {\rm{Max}}\sum\limits_f {\sum\limits_{k \in K} {\sum\limits_{j \in {\rm{CS}} \cup {\rm{NA}} \cup A} {f_{jf}^kx_{jf}^k} } } $ | (1) |
s.t:
| $ \sum\limits_{k \in K} {\beta _j^kx_{jf}^k} \le \sum\limits_{k \in K} {\beta _j^kD_{jf}^k} \forall j \in {\rm{CS}},k \in K,f \in F $ | (2) |
| $ x_{jf}^k \le D_{jf}^k + \omega _j^{ - k,k}{\left( {\sum\limits_{ - k \in K} {\beta _j^{ - k}D_{jf}^{ - k}} - \sum\limits_{ - k \in K} {\beta _j^{ - k}x_{jf}^{ - k}} } \right)^ + } $ |
| $ \forall j \in A,k \in K,f \in F $ | (3) |
| $ x_{jf}^k \le D_{jf}^k\forall j \in {\rm{NA}},k \in K,f \in F $ | (4) |
| $ \sum\limits_f {\sum\limits_{k \in K} {\sum\limits_{j \in {\rm{CS}} \cup {\rm{NA}} \cup A} {{a_{ij}}x_{jf}^k} \le } } \sum\limits_{k \in K} {c_i^k} \forall i \in L $ | (5) |
| $ x_{jf}^k \ge 0\;\;\;\forall j \in {\rm{CS}} \cup {\rm{NA}} \cup A,f \in F $ | (6) |
The objection function (1) is to maximize the total revenue of airline alliance. Constraint (2) represent the demand constraint in codeshare route, and constraint (3) represent the demand constrain with the existence of horizontal competence. Constraint (4) represent the demand constraint in the case that is not influenced by horizontal and vertical competence. Constraint (5) ensure the number of requests on each flight leg do not exceed the total seats that can be provided. Constraint (6) define the variables to be non-negative.
After solving the model, we obtain the shadow price of each flight leg corresponding to constraint (5). Shadow price means the value of scare resource. In this paper, shadow price means the value of each flight leg. Let {φi:i∈L} denote the shadow price of flight leg i calculated by above model. Then, the revenue distribution proportion αjk can be calculated as follows,
| $ \alpha _j^k = \frac{{\sum\limits_j {a_{ij}^k{{\hat \varphi }_i}} }}{{\sum\limits_j {{a_{ij}}{{\hat \varphi }_i}} }} $ | (7) |
Equation (7) implies that, the revenue distributionproportion of airline k is equal to the ratio of the sum in each flight leg's shadow price of route j which are operated by airline k and the sum of all flight legs' shadow price of route j.
2.2 Model under decentralized mechanismSince each airline under the decentralized mechanism has independent accounting for its own revenue, there will be more issues need to be considered under the decentralized mechanism than that under the centralized mechanism. In this paper, we only consider the case that two airlines operate one flight leg separately and they also both sell the tickets of codeshare route. In the previous research, the demands belong to different airlines in codeshare route were taken as a whole. Actually, each airline has its own demand in codeshare route and the ticket prices of the same codeshare route of the two airlines may also be different. Therefore, in this paper, the demand in codeshare route was taken apart, and each airline can sell the tickets with different prices.
In the process of calculation under the decentralized mechanism, the route was separated into two types, one is sold by the airline itself, represented by CSMk. The other is sold by the codeshare airline and it is only responsible for carrying, represented by CSOk. In this situation, the airline's revenue in this codeshare route is consist of two parts, the first part is fjfkαjk, j∈CSMk, and the second part is fjfkαjk, j∈CSOk. The total revenue that airline k can obtain is
| ${Z^k} = {\rm{Max}}\sum\limits_{j \in {\rm{NA}} \cup A} {\sum\limits_f {f_{jf}^kx_{jf}^k} } + \sum\limits_{j \in {\rm{CS}}_M^k \cup {\rm{CS}}_O^k} {\sum\limits_f {\alpha _j^kf_{jf}^kx_{jf}^k} } $ | (8) |
s.t:
| $ x_{jf}^k \le D_{jf}^k\forall j \in {\rm{N}}{{\rm{A}}^k},f \in F $ | (9) |
| $ x_{jf}^k \le D_{jf}^k + \omega _j^{ - k,k}{\left( {\sum\limits_{ - k \in K} {\beta _j^{ - k}D_{jf}^{ - k}} - \sum\limits_{ - k \in K} {\beta _j^{ - k}x_{jf}^{ - k}} } \right)^ + } $ |
| $ \forall j \in {A^k},f \in F $ | (10) |
| $ x_{jk}^k \le {\rm{Min}}\left\{ {D_{jf}^k,\sum\limits_k {\beta _j^kD_{jf}^k} - \beta _j^{ - k}x_{jf}^{ - k}} \right\} $ |
| $ \forall j \in {\rm{CS}}_M^k \cup {\rm{CS}}_O^k,f \in F $ | (11) |
| $ \sum\limits_f {\sum\limits_{j \in {\rm{NA}} \cup A} {{a_{ij}}x_{jf}^k} } + \sum\limits_f {\sum\limits_{j \in {\rm{CS}}_M^k \cup {\rm{CS}}_O^k} {{a_{ij}}x_{jf}^k} } \le c_i^k $ |
| $ \forall i \in {L^k},f \in F $ | (12) |
| $ x_{jf}^k \ge 0\forall j \in {\rm{C}}{{\rm{S}}^k} \cup {\rm{N}}{{\rm{A}}^k} \cup {A^k},f \in F $ | (13) |
The objection function (8) is to maximize the revenue of the single airline k. Constraints (9-11) denote the demand constrains, represent the number of sold seats that can't exceed the demand of the each route. Constraint (11) are the demand constraint of codeshare route, the number of seats that the other airline in this codeshare route can provided need to be considered, it is denoted by βj-kxjf-k. The demand was simplified with its own demand in the route, and the own demand of each airline in codeshare route is assumed to be known. Constraint (12) represent the capacity constraints. The number of seats is composed of two parts. One is the seats used on the codeshare route, the other is the seats used on the non-codeshare route. Constraint (13) are non-negative constraint, that is to say, the number of seats in each flight leg must be non-negative. Otherwise, in this calculation, the total demand of each fare class in code-share routes is no more than the capacity that the airline can provide. So, the constraint (9) and (11) can be combined into
| $ x_{jf}^k \le D_{jf}^k + \omega _j^{ - k,k}{\left( {\sum\limits_{ - k} {D_{jf}^{ - k}} - \sum\limits_{ - k} {x_{jf}^{ - k}} } \right)^ + } $ |
| $ \forall j \in {A^k} \cup {\rm{CS}}_M^k \cup {\rm{CS}}_O^k,f \in F $ | (14) |
The existence of competence will make some influence on the decision of seat inventory control and price decision. By taking horizontal and vertical competition into account, each airline can realize the revenue management closer to the reality. To control seat inventory independently by this model, the demand and capacity of other airlines in the routes which influenced by the horizontal and vertical competition also are needed to be known. However, with the development of sales system and the popularity of online ticket booking, each airline can make some assumptions of the demand and capacity according to the fare information of other airlines.
3 Numerical ExperimentsIn this section, an airline network is established to test the models built in previous sections. H1, H2, H3, H4 are four hubs in the airline network, and S1, S2, S3, S4, S5, S6, S7, S8 are spokes in the airline network. Eight airlines exist in this network, they are denoted by A1, A2, A3, A4, A5, A6, A7, A8 respectively. A1 and A2 are based in H1, A3 and A4 are based in H2, A5 and A6 are based in H3, A7 and A8 are based in H4. The routes operated by each airline are shown in Table 1.
| Table 1 Routes owned by each airline |
Among them, H1S4, H2S8, H4S6, H3S2 are codeshare routes, and H1S1, H2S3, H4S7, H3S5 are routes influenced by horizontal competition.
According to the airline network, three test sets were set. The mainly differences are reflected in the fare and capacity. Compared to the test set one, the capacity and demand of set two in the same route changed, but the fare is same. And compared to the test set one, the fare of set three in the same class of route changed, the capacity and demand didn't changed. For all airlines in network, the first class is full fare, and the second class is half fare ticket.
The route network diagram is shown as in Fig. 1.
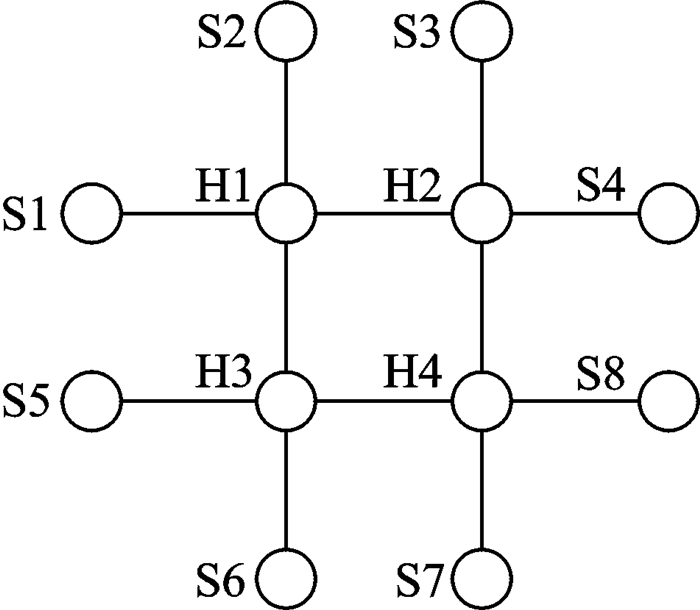
|
Fig. 1 The route network diagram |
The models proposed in Section 2 are used to solve the different test sets. The total revenue of alliance under the centralized mechanism and decentralized mechanism are shown in the Table 2. Otherwise, the revenue distribution proportions of each codeshare route are shown in Table 3. The revenue of each codeshare route under decentralized mechanism is calculated by revenue distribution proportion in Table 3. Table 4 represents the seat number of each route that each airline under the decentralized mechanism should provide.
| Table 2 Revenue results under different test scenarios |
| Table 3 Ratio value of revenue distribution on code sharing route under different scenarios |
| Table 4 Seat allocation results under different test scenarios |
As Table 1 shows, the revenue under the centralized mechanism is always better than the revenue under the decentralized mechanism, and this result is obviously consistent with the reality. The result calculated under the centralized mechanism is the upper limit of the alliance value. But, this upper limit cannot be reached because the degree of the information sharing is limited. So, the upper limit just be taken as benchmarks for comparison. The total revenue calculated under the centralized mechanism is compared with which calculated under the decentralized mechanism. Through the result of three test sets, there was a conclusion that decentralized mechanism can achieve a good result, and table three shows that the numbers of seats in the same route by each airline are closing to accordance.
4 ConclusionsThe revenue management of the airline alliance is of great significance. In a large extent, it can promote the fair distribution of revenue among airlines, ensure effective competition, and increase the overall revenue.
Being different from previous research achievements, this paper takes both of horizontal and vertical competition into account and considers the multi-fare class case at the same time to study the alliance revenue distribution problem. The demand of codeshare route was taken apart according to the different airlines. Firstly, a centralized model was built to optimize the total revenue of airline alliance. By this model, the shadow price of each flight leg can be obtained. It can be used to calculate the revenue distribution proportion. These proportion values can be used in the second model under the decentralized mechanism. Through the second model, the seat allocation results and each airline's revenue are calculated. Then, the single airline's revenue is summed to calculate the total revenue in alliance. Comparing the total revenue under the decentralized mechanism with that under the centralized mechanism, we find that, using the shadow price to calculate the model under decentralized mechanism can realize a good revenue and make a better revenue distribution. If the demand can be transferred between different airlines in the same alliance, it can increase each airline's revenue and the total revenue of alliance. That is to say, the transference of competence can increase revenue effectively. However, passenger demand and the time factor in this paper are simplified, in the future, the dynamic revenue management of airline alliance with the stochastic demand distribution can be further considered.
Acknowledgement
This paper is partially supported by the Natural Science Foundation of Jiangsu Province (No.BK 20151479) and the Central University Basic Research Fees(No. NZ2016109).
| [1] |
ALDERIGHI M, GAGGERO A, PIGA C. The effect of code-share agreements on the temporal profile of airline fares[J]. Transportation Research Part A Policy & Practice, 2015, 79: 42-54. |
| [2] |
ZOU L, CHEN X. The effect of code-sharing alliances on airline profitability[J]. Journal of Air Transport Management, 2017, 58: 50-57. DOI:10.1016/j.jairtraman.2016.09.006 |
| [3] |
BOYD E, Airline alliance revenue management[D]. OR/MS Today, 1998, 25: 28-31.
|
| [4] |
JAIN H. Alliance revenue management in practice: Techniques and simulation analysis[C]//Massachusetts Institute of Technology. Cambridge, MA, 2011: 139-142.
|
| [5] |
GRAF M, KIMMS A. An option-based revenue management procedure for strategic airline alliances[J]. European Journal of Operational Research, 2011, 215(2): 459-469. DOI:10.1016/j.ejor.2011.06.009 |
| [6] |
GRAF M, KIMMS A. Transfer price optimization for option-based airline alliance revenue management[J]. International Journal of Production Economics, 2013, 145(1): 281-93. DOI:10.1016/j.ijpe.2013.04.049 |
| [7] |
NETESSINE S, SHUMSKY R. Revenue management games:Horizontal and vertical competition[J]. Management Science, 2005, 51(5): 813-831. DOI:10.1287/mnsc.1040.0356 |
| [8] |
GRAUBERGER W, KIMMS A. Revenue management under horizontal and vertical competition within airline alliances[J]. Omega, 2016, 59(2): 228-237. |
| [9] |
KIMMS A. Approximate nucleolus-based revenue sharing in airline alliances[J]. European Journal of Operational Research, 2012, 220(2): 510-521. DOI:10.1016/j.ejor.2012.01.057 |
| [10] |
CETINERD, KIMMS A. Assessing fairness of selfish revenue sharing mechanisms for airline alliances[J]. Omega, 2013, 41(4): 641-52. DOI:10.1016/j.omega.2012.08.006 |
| [11] |
AMIGO I, BELZARENA P VATON S. Revenue sharing in network utility maximization problems[J]. Netnomics Economic Research & Electronic Networking, 2016, 17(3): 1-30. |
| [12] |
HU X, VULCANO G. Revenue sharing in airline alliances[J]. Management Science, 2013, 59(5): 1177-1195. DOI:10.1287/mnsc.1120.1591 |
| [13] |
WRIGHT C, GROENVEVELT H, SHUMSKY R. Dynamic revenue management in airline alliances[J]. Transportation Science, 2010, 44(1): 15-37. DOI:10.1287/trsc.1090.0300 |
| [14] |
RAMACHANDRAN P, VENKATARAMAN S. A bargaining framework for the airline alliance revenue sharing problem[J]. International Journal of Revenue Management, 2016, 9(4): 201-220. DOI:10.1504/IJRM.2016.079817 |
| [15] |
TOPALOGLU H. A duality based approach for network revenue management in airline alliances[J]. Journal of Revenue and Pricing Management, 2012, 11(5): 500-517. DOI:10.1057/rpm.2012.8 |
| [16] |
LE M, MA B. Aircraft and crew integrated fast optimal recovery in airline operation and control[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2015, 47(4): 487-496. |
| [17] |
ZHU B, ZHU J. Flight schedule recovery under uncertain airport capacity[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2016, 33(4): 479-490. |
 2018, Vol. 35
2018, Vol. 35


